The Orthocenter

The three altitudes of a triangle also intersect at a common point, and this point is called the "orthocenter" of the triangle.

If the triangle is acute, its orthocenter is inside:

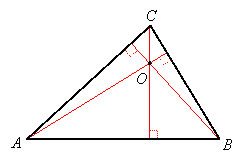
To see why the three altitudes intersect in a common point, construct a larger triangle containing the vertices of the given triangle and whose sides are parallel to the sides of the given triangle:

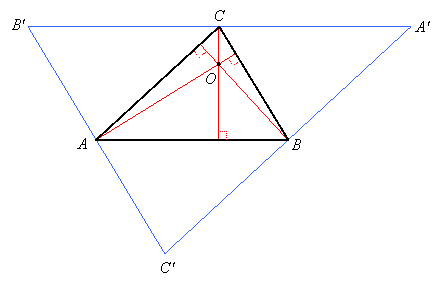
Considering alternate interior angles for parallel lines cut by transversals, we see that angle B'CA is congruent to angle A of the original triangle, angle A'CB is congruent to angle B of the original triangle, angle B'AC is congruent to angle C of the original triangle, and so on.  Since triangle B'CA shares a common side (AC) with the original triangle and has angles congruent to the angles of the original triangle, it is congruent to the original triangle, and B'C is congruent to AB.  Likewise triangle A'CB is congruent to the original triangle, and A'C is also congruent to AB.  It also follows that A'B = AC = C'B and B'A = CB = C'A.  Therefore the altitudes of triangle ABC are the perpendicular bisectors of the sides of triangle A'B'C', so they intersect at a common point which is the circumcenter of triangle A'B'C'.

The orthocenter of a right triangle is the vertex of its right angle:

The orthocenter of an obtuse triangle is outside the triangle:

 

toc | return to top | previous page