The Centers of a Triangle

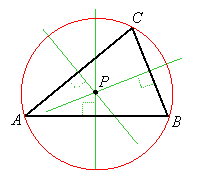
The Circumcenter

We have already seen that the three perpendicular bisectors of the sides of a triangle meet at a common point which is the center of its circumcircle:

This is true because points on a perpendicular bisector are equidistant from the endpoints of the segment it bisects, so the intersection of any two perpendicular bisectors of sides of the triangle will be equidistant from the vertices of those sides, and therefore the center of the circumcircle.

The center P of the circumcircle is called the "circumcenter" of the triangle.

The Incenter

We have also seen that the three bisectors of the angles of a triangle meet at a common point Q which is the center of the triangle's incircle:

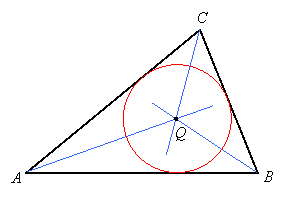
This is true because points on an angle bisector are equidistant from the sides of the angle, so the intersection of any two angle bisectors will be equidistant from the three sides of the triangle.

The Centroid

If you think of a triangle as a physical object made of wood, an important "center" would be the point where the triangle balances.  You could find that point with the following reasoning:

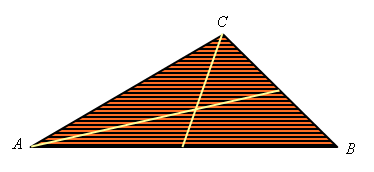
Imagine the triangle as consisting of a large number of strips parallel to one of its sides:

The balancing point (center of gravity) of each of these strips is its center, so the balancing point of the triangle would be somewhere along the line joining these centers:

This line is a median of the triangle.  If we were to think of the triangle as being composed of strips parallel to another side, we would conclude that the center of gravity is somewhere along the median to that side as well:

Therefore, the center of gravity of the triangle must be at the intersection of any two medians, and since there can only be one center of gravity, the three medians of a triangle must intersect in a common point X called the "centroid" of the triangle:

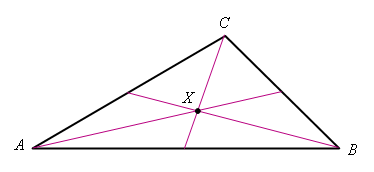
It is also a fact that the distance from a vertex to the centroid is twice the distance from the centroid to the midpoint of the opposite side.

Centroid Proof

Let D, E and F be the midpoints of sides AB, AC and BC, respectively, and let X be the intersection of medians AF and BE:

Let G and H be the midpoints of AX and BX, respectively, and consider segments EF and GH:

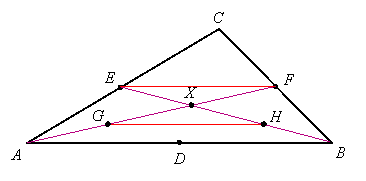
EF is a midsegment of triangle ACB, so it is parallel to AB and half as long as AB.  GH is a midsegment of triangle AXB, so it is also parallel to AB and half as long as AB.  Therefore EF and GH are parallel and of the same length.  Connecting EG and FH therefore gives us a parallelogram whose diagonals intersect at X:

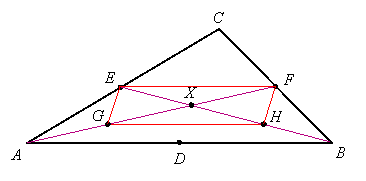
Since the diagonals of a parallelogram bisect each other, this tells us GX = FX and EX = HX.  But G and H are the midpoints of AX and BX, so we now know that AX = 2FX and BX = 2EX.  In other words, the distance from a vertex to the point of intersection of any two medians is twice the distance from that intersection to the midpoint of the opposite side.  Therefore each median contains a common point of trisection, and the three medians concur.

The Orthocenter

The three altitudes of a triangle also intersect at a common point, and this point is called the "orthocenter" of the triangle.

If the triangle is acute, its orthocenter is inside:

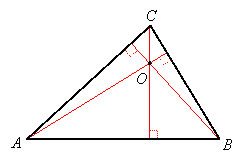
To see why the three altitudes intersect in a common point, construct a larger triangle containing the vertices of the given triangle and whose sides are parallel to the sides of the given triangle:

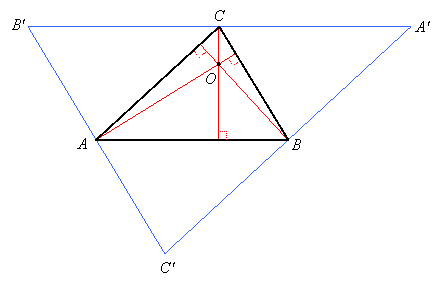
Considering alternate interior angles for parallel lines cut by transversals, we see that angle B'CA is congruent to angle A of the original triangle, angle A'CB is congruent to angle B of the original triangle, angle B'AC is congruent to angle C of the original triangle, and so on.  Since triangle B'CA shares a common side (AC) with the original triangle and has angles congruent to the angles of the original triangle, it is congruent to the original triangle, and B'C is congruent to AB.  Likewise triangle A'CB is congruent to the original triangle, and A'C is also congruent to AB.  It also follows that A'B = AC = C'B and B'A = CB = C'A.  Therefore the altitudes of triangle ABC are the perpendicular bisectors of the sides of triangle A'B'C', so they intersect at a common point which is the circumcenter of triangle A'B'C'.

The orthocenter of a right triangle is the vertex of its right angle:

The orthocenter of an obtuse triangle is outside the triangle: