The Centroid

If you think of a triangle as a physical object made of wood, an important "center" would be the point where the triangle balances.  You could find that point with the following reasoning:

 

Imagine the triangle as consisting of a large number of strips parallel to one of its sides:

The balancing point (center of gravity) of each of these strips is its center, so the balancing point of the triangle would be somewhere along the line joining these centers:

This line is a median of the triangle.  If we were to think of the triangle as being composed of strips parallel to another side, we would conclude that the center of gravity is somewhere along the median to that side as well:

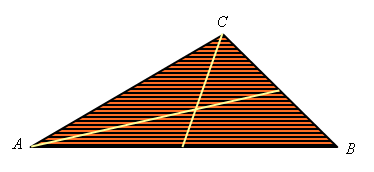
Therefore, the center of gravity of the triangle must be at the intersection of any two medians, and since there can only be one center of gravity, the three medians of a triangle must intersect in a common point X called the "centroid" of the triangle:

 

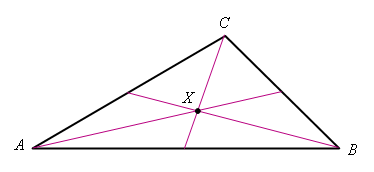
It is also a fact that the distance from a vertex to the centroid is twice the distance from the centroid to the midpoint of the opposite side.

toc | return to top | previous page | next page