Centroid Proof

Let D, E and F be the midpoints of sides AB, AC and BC, respectively, and let X be the intersection of medians AF and BE:

Let G and H be the midpoints of AX and BX, respectively, and consider segments EF and GH:

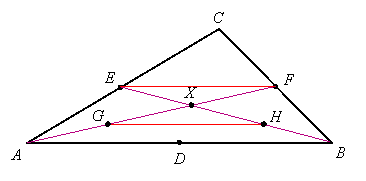
EF is a midsegment of triangle ACB, so it is parallel to AB and half as long as AB.  GH is a midsegment of triangle AXB, so it is also parallel to AB and half as long as AB.  Therefore EF and GH are parallel and of the same length.  Connecting EG and FH therefore gives us a parallelogram whose diagonals intersect at X:

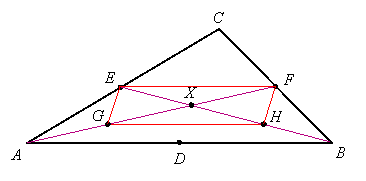
Since the diagonals of a parallelogram bisect each other, this tells us GX = FX and EX = HX.  But G and H are the midpoints of AX and BX, so we now know that AX = 2FX and BX = 2EX.  In other words, the distance from a vertex to the point of intersection of any two medians is twice the distance from that intersection to the midpoint of the opposite side.  Therefore each median contains a common point of trisection, and the three medians concur.

toc | return to top | previous page | next page