Example 6:  Points A and B are 10 units apart.  A point X is chosen on an arc with endpoints A and B, and points P and Q are located on the same side of this arc so that angles PAX and PBX are right angles, AP = AX, and BQ= BX.  Then the midpoint M of PQ is located:

What is the locus of M as X moves from A to B along the arc?

Solution: 

Draw PD, XC, MN, and QE perpendicular to AB:

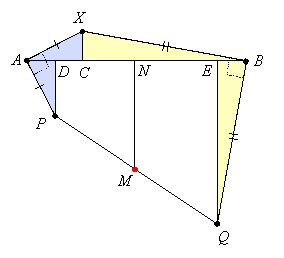
Then triangles ACX and PDA are congruent, as are triangles BCX and QEB.  So XC = AD and XC = BE.  Since M is the midpoint of side PQ in trapezoid DPQE (the white region), MN is its midsegment and therefore its length is the average of lengths DP and EQ.  But DP = AC and EQ = CB, so DP + EQ = AB = 10, and therefore MN = 5.  But N is the midpoint of DE and therefore the midpoint of AB (since AD = EB).  Thus M is 5 units below (perpendicular) AB's midpoint.  That is, the locus does not depend on the location of X and is a single point.  The fact that X is on some arc connecting A and B is irrelevant.

toc | return to top | previous page