Locus Problems

Locus

"Locus" is a Latin word for "place."  Its plural is "loci."  In geometry, "locus" refers to a set of points that are described by some statement about their position.  For example, the locus of points that are 1 unit from point A refers to the set of all points that are 1 unit from point A.  This would be the circle with center A:

Some locus problems are restatements of theorems in geometry, such as the following examples.

Example 1:  What is the locus of points that are equidistant from the sides of an angle?

Answer:  This locus is the angle bisector:

Example 2:  What is the locus of points equidistant from two given points?

Answer:  This locus is the perpendicular bisector of the segment containing those points as its endpoints:

Example 3:  Given 2 points A and B, what is the locus of points P so that angle APB is a right angle?

Answer:  The circle with diameter AB, excluding points A and B.  (Remember?  An angle inscribed in a semicircle is a right angle.) 

Example 4:  A 10-foot ladder is placed vertically against a wall, and then the foot of the ladder is moved outward until the ladder lies flat on the floor with one end touching the wall.  What is the locus of the midpoint of the ladder as it slides?

Solution:  The first thing to do is carefully draw some cases to get an idea of what that locus might be:

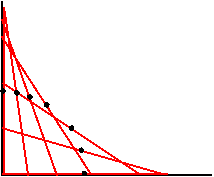
It appears that the points are on an arc of a circle, so let's look at one of the points:

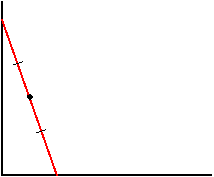
The midpoint is on the hypotenuse of the right triangle whose legs are on the wall and floor.  Since a right triangle can be inscribed in a semicircle with the midpoint of the hypotenuse as its center, we know the distance OM is a radius of this circle and therefore 5 feet:

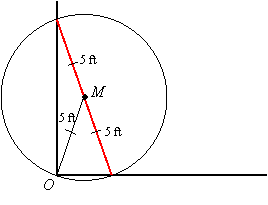That is, no matter where the ladder is, OM will be 5 feet, and therefore the locus of midpoints is a quarter of a circle with center at the intersection of the floor and wall (point O) and radius 5 feet:

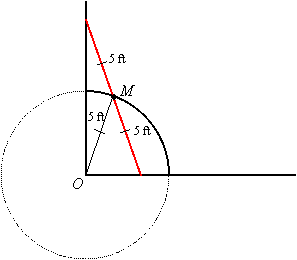
Locus problems in geometry sometimes involve two or more conditions, as the following examples illustrate.

Example 5:  If A and B are two points that are 2 units apart, what is the locus of points that are 1 unit from A and 2 units from B?

Solution:  The locus of points that are 1 unit from A is the circle with center A and radius 1.  The locus of points that are 2 units from B is the circle with center B and radius 2.  Therefore, the locus of points that are 1 unit from A and 2 units from B is the intersection of these two circles:

Example 6:  Points A and B are 10 units apart.  A point X is chosen on an arc with endpoints A and B, and points P and Q are located on the same side of this arc so that angles PAX and PBX are right angles, AP = AX, and BQ= BX.  Then the midpoint M of PQ is located:

What is the locus of M as X moves from A to B along the arc?

Solution: 

Draw PD, XC, MN, and QE perpendicular to AB:

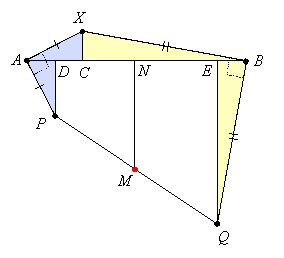
Then triangles ACX and PDA are congruent, as are triangles BCX and QEB.  So XC = AD and XC = BE.  Since M is the midpoint of side PQ in trapezoid DPQE (the white region), MN is its midsegment and therefore its length is the average of lengths DP and EQ.  But DP = AC and EQ = CB, so DP + EQ = AB = 10, and therefore MN = 5.  But N is the midpoint of DE and therefore the midpoint of AB (since AD = EB).  Thus M is 5 units below (perpendicular) AB's midpoint.  That is, the locus does not depend on the location of X and is a single point.  The fact that X is on some arc connecting A and B is irrelevant.

Return to Lesson