Example 4: A 10-foot ladder is placed vertically against a wall, and then the foot of the ladder is moved outward until the ladder lies flat on the floor with one end touching the wall. What is the locus of the midpoint of the ladder as it slides?
Solution: The first thing to do is carefully draw some cases to get an idea of what that locus might be:
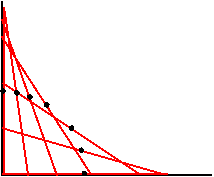
It appears that the points are on an arc of a circle, so let's look at one of the points:
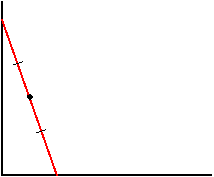
The midpoint is on the hypotenuse of the right triangle whose legs are on the wall and floor. Since a right triangle can be inscribed in a semicircle with the midpoint of the hypotenuse as its center, we know the distance OM is a radius of this circle and therefore 5 feet:
 |
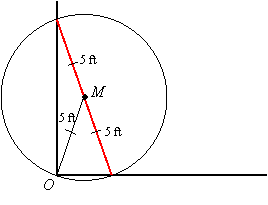That is, no matter where the ladder is, OM will be 5 feet, and therefore the locus of midpoints is a quarter of a circle with center at the intersection of the floor and wall (point O) and radius 5 feet:
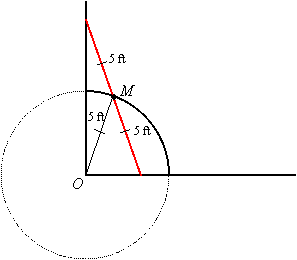
Locus problems in geometry sometimes involve two or more conditions, as the following examples illustrate.
Content ©2008. All Rights Reserved.
Date last modified: March 5, 2009.