- Prev
- Page 6 of 6
Regular Polygons and Archimedes' Computation of pi
Any regular polygon can be inscribed in a circle. This is intuitively obvious, so we will not try to "prove" it. The center of the circle for a polygon with an even number of sides is the intersection of any two diagonals, and the center of the circle for a polygon with an odd number of sides is the intersection of any two angle bisectors:
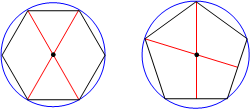
Archimedes used inscribed polygons to approximate the value of π. He started with a regular hexagon with sides that are 1 unit. Then the radius of the circle containing the hexagon is 1 unit (triangle AOB is equilateral since its angles are 60o):

Then he constructed OQ through the midpoint P of segment AB:
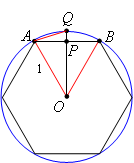
Notice that triangles OAP and OBP are congruent by SSS, so angle APO is a right angle.
Now look at triangles OAQ and OAP. Since P was the midpoint of AB, AP is ½ unit in length.

By the Pythagorean Theorem, we can find OP, and therefore CP:
OP2 + (½)2 = 12
OP2 = ¾ = 0.75
OP = 0.8660254
Since OQ is a radius of the circle, its length is 1, so QP = 1 – OP = 0.1339746.
Now use the Pythagorean Theorem on triangle APC to find AC:
AQ2 = (½)2 + (0.1339746)2 = 0.26794919
AQ = 0.51763809
This is the length of a side of the dodecagon (12-sided polygon) inscribed in the unit circle:
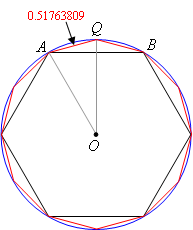
The perimeter of the dodecagon is close to the circumference of the circle. This perimeter is 12 times 0.5176389, or 6.2116571. Since pi is the circumference divided by the diameter, we get an approximate value of 3.10582854.
Now Archimedes did not stop there. He next did the same construction using the dodecagon. Let OQ' be a radius that intersects side AQ of the dodecagon at its midpoint:
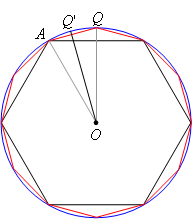
Now we have:
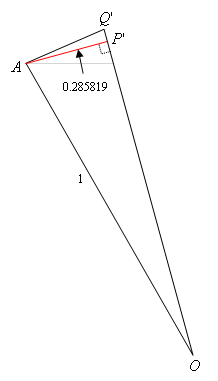
AP' is half of 0. 0.51763809, or 0.285819. Using the Pythagorean Theorem on triangle AP'O we find that OP' = 0.9659258, so Q'P' = 1 – 0.9659258 = 0.0340742, and then using the Pythagorean Theorem on triangle AP'Q', we find that AQ' = 0.2610524.
AD is a side of the regular 24-gon inscribed in circle O, and the perimeter of that polygon is 24(0.2610524) = 6.2652572. This is closer to the circumference of the circle, so now we estimate pi to be 3.132629.
The following table illustrates this procedure carried out to 8 steps, where n is the number of sides of the inscribed polygon:
