Inscribed Triangles
All triangles can be inscribed in a circle, and the center of the circle is the intersection of any two perpendicular bisectors of its sides. This works because points on the perpendicular bisector of a segment are equidistant from its endpoints:
Given: Triangle ABC is inscribed in a circle
Prove: The center of that circle is at the point of intersection of the perpendicular bisectors of AB and AC.
Proof: Let P be the intersection of those two perpendicular bisectors. Every point on the perpendicular bisector of AB is equidistant from A and B, so P is equidistant from A and B:
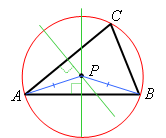
Likewise, every point on the perpendicular bisector of AC is equidistant from A and C, so P is also equidistant from these points:
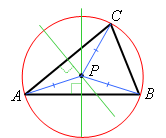
Therefore P is the center of the circle (since a circle is defined as the set off all points equidistant from the center), and the common distance PA = PB = PC is the radius of the circle.
Had we chosen to use the perpendicular bisectors of AB and BC instead, we would get the same result, since there can only be one center of a circle. So a consequence of this is that the perpendicular bisectors of the sides of any triangle must meet at a common point.
The circle in which the triangle is inscribed is called its circumcircle, and we can also say that the circle has been circumscribed about the triangle. The center of that circle is called the circumcenter of the triangle.
Content ©2008. All Rights Reserved.
Date last modified: May 24, 2009.