
Inscribed Polygons
Inscribed Polygons
A polygon is said to be inscribed in a circle if all its vertices are on the circumference of the circle. Not every polygon can be inscribed in a circle. For example, a parallelogram (which is not a rectangle) cannot be inscribed in a circle, because a circle containing three of its vertices cannot contain the fourth:

A polynomial that can be inscribed in a circle is called a cyclic polynomial. For example, the following pentagon is cyclic:


Inscribed Triangles
All triangles can be inscribed in a circle, and the center of the circle is the intersection of any two perpendicular bisectors of its sides. This works because points on the perpendicular bisector of a segment are equidistant from its endpoints:
Given: Triangle ABC is inscribed in a circle

Prove: The center of that circle is at the point of intersection of the perpendicular bisectors of AB and AC.
Proof: Let P be the intersection of those two perpendicular bisectors. Every point on the perpendicular bisector of AB is equidistant from A and B, so P is equidistant from A and B:
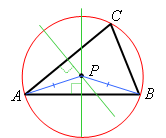
Likewise, every point on the perpendicular bisector of AC is equidistant from A and C, so P is also equidistant from these points:
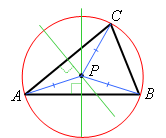
Therefore P is the center of the circle (since a circle is defined as the set off all points equidistant from the center), and the common distance PA = PB = PC is the radius of the circle.
Had we chosen to use the perpendicular bisectors of AB and BC instead, we would get the same result, since there can only be one center of a circle. So a consequence of this is that the perpendicular bisectors of the sides of any triangle must meet at a common point.
The circle in which the triangle is inscribed is called its circumcircle, and we can also say that the circle has been circumscribed about the triangle. The center of that circle is called the circumcenter of the triangle.

An Application
The idea of finding the circumcenter of a triangle using perpendicular bisectors of its sides has an important application in archaeology:
While on an archaeological dig, Fred uncovered a piece of a circular dish. He wanted to know how big the original dish was, so he needed to determine its diameter.

To do this, he laid the piece on a coordinate plane with gridlines spaced 1 cm apart, and found three points on the dish's edge were at coordinates (0, 0), (–4, 2), and (6, 2).

These three points determine a triangle with those vertices, so he found the equations of two perpendicular bisectors of the sides, set their y-values equal to find their point of intersection, and then was able to find the radius as the hypotenuse of a right triangle from that point to the origin:

The line through (0, 0) and (–4, 2) has slope –2/4 = –1/2, so the perpendicular bisector has slope 2. The midpoint has coordinates (–2, 1), so the equation of the perpendicular bisector is y – 1 = 2(x + 2) which simplifies to y = 2x + 5.
The line through (0, 0) and (6, 2) has slope 2/6 = 1/3, so the perpendicular bisector has slope –3. The midpoint has coordinates (3, 1), so the equation of the other perpendicular bisector is y – 1 = –3(x – 3) which simplifies to y = –3x + 10.
If we set the y's of these two lines equal to each other, we have:
2x + 5 = –3x + 10
Solving this we get x = 1. We can use either line's equation to find y, and we get y = 7. So the point (1, 7) is center of the circle, and we can now find the radius since it is the distance from the center to any of the three vertices of the triangle.
The distance from (1, 7) to (0, 0) is
![]()
or about 7.07 cm.
Therefore the diameter is about 14.14 cm.


Inscribed Quadrilaterals
As we mentioned before, not all quadrilaterals can be inscribed in a circle. A quadrilateral that can be inscribed in a circle is called a cyclic quadrilateral. The main result about cyclic quadrilaterals is:
Opposite angels of a cyclic quadrilateral are supplementary, and conversely.
To see why this must be so, suppose ABCD is a cyclic quadrilateral inscribed in circle O:

Then angle A measures half of arc BCD and angle C measures half of arc DAB since these are inscribed angles. But arcs BCD and DAB add to 360o, so angles A and C add to 180o. Likewise, angles B and D add to 180o, which proves opposite angles of a cyclic quadrilateral are supplementary.
The converse is also true:
Suppose opposite angles of quadrilateral ABCD are supplementary. That is, angles A and C are supplementary, and angles B and D are supplementary: Triangle BCD is cyclic, so construct the circle which contains it. Suppose A does not lie on that circle:

Then let P be the point of intersection of AB with that circle, and draw segment DP:

Since quadrilateral PBCD is cyclic, angle DPB is supplementary to angle C. But since angle A is also supplementary to angle C, angles DPB and A are congruent. But angle DPB is an exterior angle of triangle APD, so it would have to be greater than the interior angle A. This is a contradiction, so it must be the case that A lies outside the circle. By a similar argument, it is easy to show that A cannot lie inside that circle either, so it must be that A lies on that circle, and therefore ABCD is cyclic.

Ptolomy's Theorem
Let ABCD be a cyclic quadrialteral. Ptolomy's Theorem says that the product of the diagonal lengths equals the sum of the product of the lengths of opposite sides:
AC . BD = AB . CD + BC . AD

Proof:
Notice the angles ACB and ADB are congruent since they intercept the same arc (arc AB). Let P be the point on BD such that angle PCD is congruent to angles ACB and ADB.

In triangles ABC and DPC, angles BAC and BDC are congruent because they both share arc BC, and angles BCA and PCD are congruent by our choice of point P. So these triangles are similar by AA and we can write the proportion:
![]()
Cross-multiplying gives us:
![]()
Also notice that triangle BPC is similar to triangle ADC by AA, so we also know:
![]()
and therefore
![]()
Putting this together, we have:
![]()

Regular Polygons and Archimedes' Computation of pi
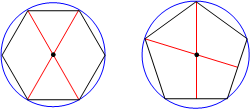
Any regular polygon can be inscribed in a circle. This is intuitively obvious, so we will not try to "prove" it. The center of the circle for a polygon with an even number of sides is the intersection of any two diagonals, and the center of the circle for a polygon with an odd number of sides is the intersection of any two angle bisectors:
Archimedes used inscribed polygons to approximate the value of π. He started with a regular hexagon with sides that are 1 unit. Then the radius of the circle containing the hexagon is 1 unit (triangle AOB is equilateral since its angles are 60o):

Then he constructed OQ through the midpoint P of segment AB:
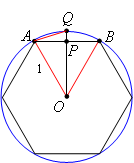
Notice that triangles OAP and OBP are congruent by SSS, so angle APO is a right angle.
Now look at triangles OAQ and OAP. Since P was the midpoint of AB, AP is ½ unit in length.

By the Pythagorean Theorem, we can find OP, and therefore CP:
OP2 + (½)2 = 12
OP2 = ¾ = 0.75
OP = 0.8660254
Since OQ is a radius of the circle, its length is 1, so QP = 1 – OP = 0.1339746.
Now use the Pythagorean Theorem on triangle APC to find AC:
AQ2 = (½)2 + (0.1339746)2 = 0.26794919
AQ = 0.51763809
This is the length of a side of the dodecagon (12-sided polygon) inscribed in the unit circle:
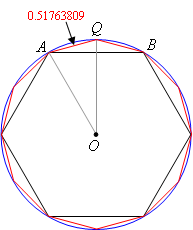
The perimeter of the dodecagon is close to the circumference of the circle. This perimeter is 12 times 0.5176389, or 6.2116571. Since pi is the circumference divided by the diameter, we get an approximate value of 3.10582854.
Now Archimedes did not stop there. He next did the same construction using the dodecagon. Let OQ' be a radius that intersects side AQ of the dodecagon at its midpoint:
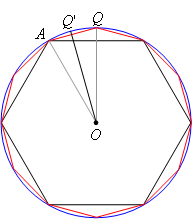
Now we have:
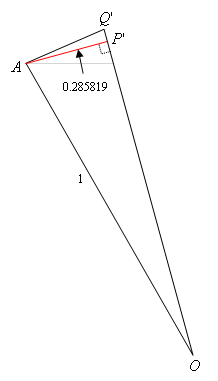
AP' is half of 0. 0.51763809, or 0.285819. Using the Pythagorean Theorem on triangle AP'O we find that OP' = 0.9659258, so Q'P' = 1 – 0.9659258 = 0.0340742, and then using the Pythagorean Theorem on triangle AP'Q', we find that AQ' = 0.2610524.
AD is a side of the regular 24-gon inscribed in circle O, and the perimeter of that polygon is 24(0.2610524) = 6.2652572. This is closer to the circumference of the circle, so now we estimate pi to be 3.132629.
The following table illustrates this procedure carried out to 8 steps, where n is the number of sides of the inscribed polygon:
