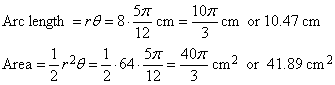Arcs and Sectors

A sector of a circle is a region bounded by two radii and an arc of the circle.  The central angle of a sector is the angle formed by the two rays and has the same measure as the arc.  When that measure is given in radians, the arc's length is the same as the radius times the central angle.  This is a direct consequence of the definition of radian measure.  Another consequence of that definition is the area of a sector is half the square of the radius times the measure of the central angle in radians:

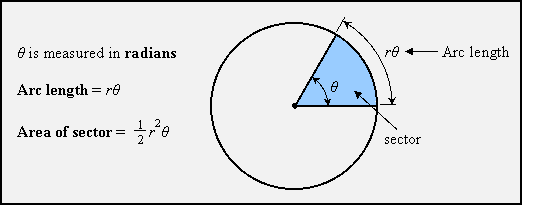
Example:  Find the arc length and area of a sector with a radius of 8 cm and a central angle of 75^o.

Solution:

First we must convert 75^o to radians:

Now we can use the formulas:

toc | return to top | previous page