Radian Measure
Degree measure of angles is not a "natural measure" as it was invented some 2,000 years ago out of an arbitrary choice of units. In some applications, it is easier to associate the measure of an angle with the length of an arc of a circle centered at the vertex of the angle. This is the idea of radian measure, and one radian is defined as the measure of an angle in standard position whose terminal side intercepts an arc of length r units in a circle of radius r with its center at the origin:
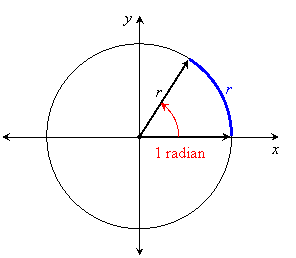
If the radius of the measuring circle is taken as 1 unit, then the length of the intercepted arc is the radian measure of the angle.
Because the circumference of a circle of radius r is 2πr, there are 2π radians in a full circle. Therefore, 360o = 2π radians, and 180o = π radians. There is no standard symbol for radian measure, but when used it is customary to just give the pure number. Thus if a problem says an angle measure is 2, then the meaning is that the angle measures 2 radians.
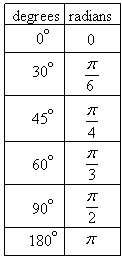
The following degree and radian measures are helpful to know:
In general, since 180o = π radians, the following rules can be used to convert angle measures:
Content ©2008. All Rights Reserved.
Date last modified: May 20, 2009.