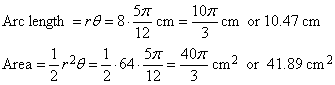
General Angles and Radian Measure

General Angles and Standard Position

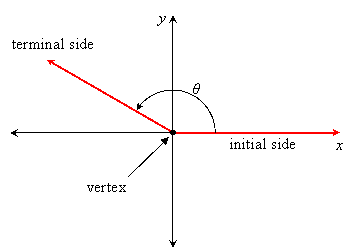
The precise definition of an angle is the union of two rays with a common vertex.  When we measure angles in degrees, we place a circle at the vertex and count the number of marks out of 360 on the circle that are interior to the angle.  This always gives us a number between 0 and 180, and that is what we might call the "protractor measure" of the angle.

There are applications, such as rotating wheels, where it is convenient to expand our definition of angle so measures can be any number of degrees, including positive and negative values.  Such a definition is given as follows:

Fix one ray, called the initial side, and place a copy of this ray on top of itself.  Then rotate the new ray, called the terminal side, about its vertex any specified number of degrees (marks on a circle which contains 360 marks and whose center is at the vertex) counterclockwise, or clockwise if the degrees are indicated by a negative number.  When the initial side is place along the positive x-axis with its vertex at the origin, the angle is said to be in standard position:

Here are some examples of angles drawn in standard position:

Coterminal Angles

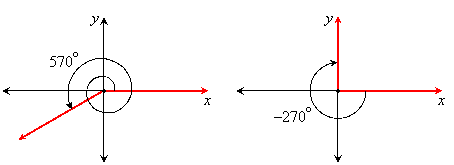
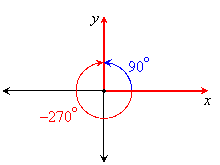
Two angles in standard position are coterminal if their terminal sides coincide.  For example, 270^o and 90^o are coterminal angles since they share the positive y axis as their terminal sides:

570^o and –150^o are also coterminal angles:

In general, two angles are coterminal if their measures differ by some multiple of 360^o.

Radian Measure

Degree measure of angles is not a "natural measure" as it was invented some 2,000 years ago out of an arbitrary choice of units.  In some applications, it is easier to associate the measure of an angle with the length of an arc of a circle centered at the vertex of the angle.  This is the idea of radian measure, and one radian is defined as the measure of an angle in standard position whose terminal side intercepts an arc of length r units in a circle of radius r with its center at the origin:

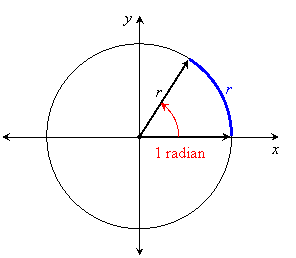
If the radius of the measuring circle is taken as 1 unit, then the length of the intercepted arc is the radian measure of the angle.

Because the circumference of a circle of radius r is 2πr, there are 2π radians in a full circle.  Therefore, 360^o = 2π radians, and 180^o = π radians.  There is no standard symbol for radian measure, but when used it is customary to just give the pure number.  Thus if a problem says an angle measure is 2, then the meaning is that the angle measures 2 radians.

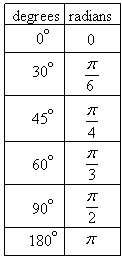
The following degree and radian measures are helpful to know:

In general, since 180^o = π radians, the following rules can be used to convert angle measures:

Arcs and Sectors

A sector of a circle is a region bounded by two radii and an arc of the circle.  The central angle of a sector is the angle formed by the two rays and has the same measure as the arc.  When that measure is given in radians, the arc's length is the same as the radius times the central angle.  This is a direct consequence of the definition of radian measure.  Another consequence of that definition is the area of a sector is half the square of the radius times the measure of the central angle in radians:

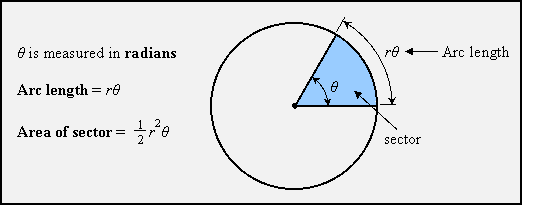
Example:  Find the arc length and area of a sector with a radius of 8 cm and a central angle of 75^o.

Solution:

First we must convert 75^o to radians:

Now we can use the formulas: