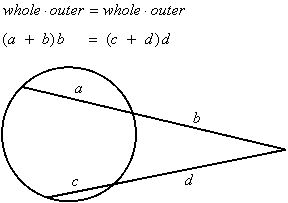
Secants from a Common External Point

Two secants that intersect in a common external point have subsegments determined by their intersections with a circle:

Secant AP has subsegments AB and BP, and secant CP has subsegments CD and DP.

If we draw chords AD and BC, we have two similar triangles, triangle APD and triangle CPB: 

These triangles are similar by AA since they share angle P, and angles DAP and BCP are inscribed angles that share arc BD.  Therefore we can write the following proportions using corresponding sides of these two triangles:

Cross-multiplying gives us the following result:

In other words, the product of the whole segment with its outer subsegment for one secant will equal the product of the whole segment with its outer subsegment for the other secant:

 

 

toc | return to top | previous page | next page