Intersecting Chords

In the previous lesson we saw that two intersecting chords determine four arcs in a circle.  The measures of these arcs are related to the angles at the intersection of the chords by the formula,

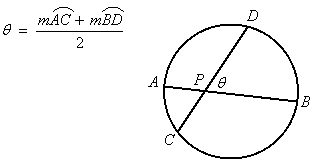Now we will consider lengths of the subsegments resulting from the intersection of these two chords:

If we draw chords AD and CB, we have triangles APD and CPB:

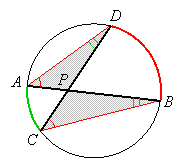Since angles DAB and DCB are inscribed angles with the common arc DB, they are congruent.  Likewise, angles ADC and CBA are congruent.  Therefore, triangles APD and CPB are similar, so their sides are proportional.  In particular, the following proportion is correct:

If we cross-multiply, we get: 

More simply, if one if the segments has subsegment lengths a and b, and the other has subsegment lengths c and d, then: 

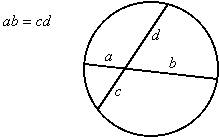toc | return to top | previous page | next page