
Chords and Secants
Arcs and Chords
In the circle shown below, chord AB cuts off two arcs, the minor arc from A to B in red and the major arc in blue. The minor arc is called the arc of chord AB.
 |
An important relation between chords and their arcs is:
Theorem 1: In the same circle or in congruent circles, congruent chords have congruent arcs, and conversely.
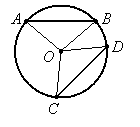 |
Proof: If we draw radii to the endpoints of the chords, we can show the resulting triangles are congruent if the chords are congruent (which gives us the SSS case) or if the arcs are congruent (so the central angles are congruent, giving the SAS case):
If chord AB is congruent to chord CD, then triangle AOB is congruent to triangle COD by SSS. Therefore angles AOB and COD are congruent, so their intercepted arcs are congruent.
Conversely, if arcs AB and CD are congruent, then the central angles AOB and COD are congruent. Therefore triangles AOB and COD are congruent by SAS, so their corresponding sides, AB and CD are congruent.
Example 1: Find the measure of angle CED:
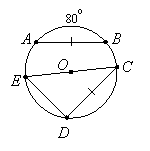 |
Solution: Since chords AB and CD are congruent, their corresponding arcs are congruent so arc CD measures 80o. Angle CED is an inscribed angle, so it measures half its intercepted arc. Therefore its measure is 40o.
Chords Equidistant from the Center
Theorem 2: If two chords are equidistant from the center of a circle, then they and their arcs are congruent, and conversely.
Proof: The distance from a chord to the center of its circle is the length of the perpendicular segment from the chord to the center.
If OP and OQ are congruent, then triangles AOP, POP, COQ, and DOQ are all congruent by HL. Therefore, segments AP, BP, CQ, and DQ are all congruent. Since AB = AP + BP and CD = CQ + DQ, it follows that segments AB and CD are congruent. By the previous theorem, their corresponding arcs must also be congruent.
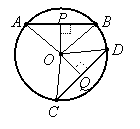 |
Conversely, if segments AB and CD are congruent (or if their arcs are congruent, which implies the segments are congruent by the previous theorem), then isosceles triangles AOB and COD are congruent, so angles OAP, OBP, OCQ, ODQ are all congruent, so right triangles AOP, BOP, COQ, and DOQ are all congruent by SAA. Therefore PQ and QO are congruent.
It also follows (from the proof of this theorem) that a radius or diameter which is perpendicular to a chord bisects that chord, and conversely:
If OP bisects AB then it is perpendicular to AB, and if OP is perpendicular to AB then it bisects AB.
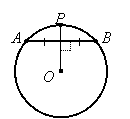 |
Example 2: Find the radius of circle O:
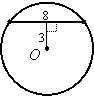 |
Solution: Since the segment from the center to the chord is perpendicular to the chord, it bisects the chord. If we draw a radius to an endpoint of the chord, we have a right triangle, so we can use the Pythagorean Theorem to find the radius:
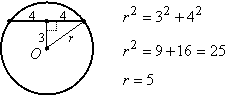 |
Intersecting Chords
In the previous lesson we saw that two intersecting chords determine four arcs in a circle. The measures of these arcs are related to the angles at the intersection of the chords by the formula,
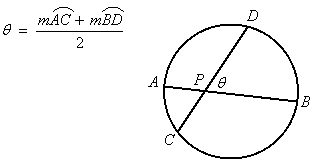 |
Now we will consider lengths of the subsegments resulting from the intersection of these two chords:
If we draw chords AD and CB, we have triangles APD and CPB:
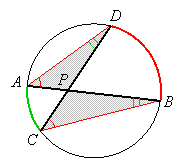 |
Since angles DAB and DCB are inscribed angles with the common arc DB, they are congruent. Likewise, angles ADC and CBA are congruent. Therefore, triangles APD and CPB are similar, so their sides are proportional. In particular, the following proportion is correct:
![]()
If we cross-multiply, we get:
![]()
More simply, if one if the segments has subsegment lengths a and b, and the other has subsegment lengths c and d, then:
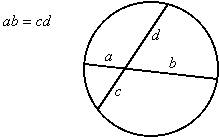 |
Example 3: Find x:
 |
Solution: The products of the subsegments of each chord are equal, so
![]()
Therefore x = 4
Secants from a Common External Point
Two secants that intersect in a common external point have subsegments determined by their intersections with a circle:
Secant AP has subsegments AB and BP, and secant CP has subsegments CD and DP.
 |
If we draw chords AD and BC, we have two similar triangles, triangle APD and triangle CPB:
 |
These triangles are similar by AA since they share angle P, and angles DAP and BCP are inscribed angles that share arc BD. Therefore we can write the following proportions using corresponding sides of these two triangles:
![]()
Cross-multiplying gives us the following result:
![]()
In other words, the product of the whole segment with its outer subsegment for one secant will equal the product of the whole segment with its outer subsegment for the other secant:
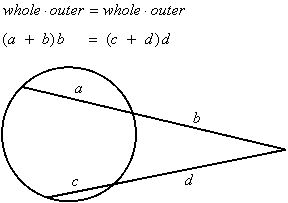
Example 4: Find x:
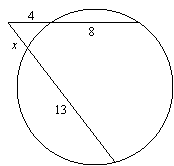 |
Solution:
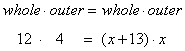
So x2 + 13x = 48
x2 + 13x – 48 = 0
(x – 3)(x + 16) = 0
x = 3 or x = –16
Since x is a segment length, it cannot be negative. Therefore, x = 3.
A Tangent and a Secant from an External Point
A similar result is true when we replace one of the secants with a tangent. The whole tangent can be thought of as its own "outer subsegment":
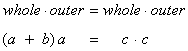
 |
Example 5: PA is tangent to the circle at point A. Find x:
 |
Solution: (x + 4)(x + 4) = (x + 12)x
So x2 + 8x + 16 = x2 + 12x
Subtracting x2 from both sides gives
8x + 16 = 12x
So 4x = 16, and we get x = 4.
Return to Lesson 7