Arcs and Chords

In the circle shown below, chord AB cuts off two arcs, the minor arc from A to B in red and the major arc in blue.  The minor arc is called the arc of chord AB.

An important relation between chords and their arcs is:

Theorem 1:  In the same circle or in congruent circles, congruent chords have congruent arcs, and conversely.

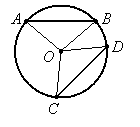Proof:  If we draw radii to the endpoints of the chords, we can show the resulting triangles are congruent if the chords are congruent (which gives us the SSS case) or if the arcs are congruent (so the central angles are congruent, giving the SAS case):

If chord AB is congruent to chord CD, then triangle AOB is congruent to triangle COD by SSS.  Therefore angles AOB and COD are congruent, so their intercepted arcs are congruent.

Conversely, if arcs AB and CD are congruent, then the central angles AOB and COD are congruent.  Therefore triangles AOB and COD are congruent by SAS, so their corresponding sides, AB and CD are congruent.

toc | return to top | next page