Chords Equidistant from the Center

Theorem 2:  If two chords are equidistant from the center of a circle, then they and their arcs are congruent, and conversely.

Proof:  The distance from a chord to the center of its circle is the length of the perpendicular segment from the chord to the center. 

If OP and OQ are congruent, then triangles AOP, POP, COQ, and DOQ are all congruent by HL.  Therefore, segments AP, BP, CQ, and DQ are all congruent.  Since AB = AP + BP and CD = CQ + DQ, it follows that segments AB and CD are congruent.  By the previous theorem, their corresponding arcs must also be congruent.

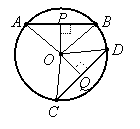Conversely, if segments AB and CD are congruent (or if their arcs are congruent, which implies the segments are congruent by the previous theorem), then isosceles triangles AOB and COD are congruent, so angles OAP, OBP, OCQ, ODQ are all congruent, so right triangles AOP, BOP, COQ, and DOQ are all congruent by SAA.  Therefore PQ and QO are congruent.

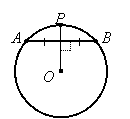
It also follows (from the proof of this theorem) that a radius or diameter which is perpendicular to a chord bisects that chord, and conversely:

If OP bisects AB then it is perpendicular to AB, and if OP is perpendicular to AB then it bisects AB.

toc | return to top | previous page | next page