Euclid's Proof of the ASA Theorem
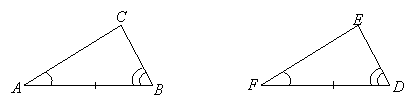SSS and ASA follow logically from SAS. Here we will give Euclid's proof of one of them, ASA. It involves indirect reasoning to arrive at the conclusion that 
must equal 
in the diagram, from which it follows (from SAS) that the triangles are congruent:
Theorem: If (see the diagram) 
, 
, and 
,
then 
.
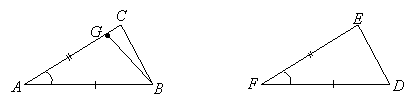Proof: Suppose 
and 
, and suppose 
is not equal to 
. Then one of these segments is longer than the other. Without loss of generality, we can suppose the longer segment is 
(because otherwise we could just relabel everything). We can then choose a point G on 
for which 
, and then construct segment 
:
By SAS it then follows that 
. This implies that 
since these are corresponding parts of the congruent triangles. But 
is part of 
, and therefore smaller than it, and so 
(which is the same size as 
) is smaller than 
.
So if 
then 
. The contrapositive of this says, if 
then 
. Therefore, if we have the three givens of our theorem (if 
, 
, and 
), then we also have 
, and so by SAS it follows that 
.
Content ©2008. All Rights Reserved.
Date last modified: October 10, 2008.