Triangles
Triangle Congruence
A triangle is a closed figure consisting of 3 angles and 3 sides. The sides are segments and meet at their vertices. We name a triangle by listing its three vertices. Two triangles are congruent if they have the same size and shape. In naming congruent triangles we must list the vertices in a consistent order, and we use an equals-sign with a wiggle over it. For example, if A, B and C are the vertices of one triangle, and D, E and F are the vertices of another triangle that is congruent to the first one, then only one of the following six possible congruences can be true:
![]() or
or ![]() or
or ![]() or
or
![]() or
or ![]() or
or ![]()
Each implies a different correspondence of the vertices. If the triangles are these:
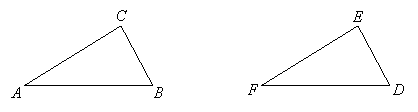
then the correct congruence is: ![]() . This means that vertex A of the first triangle matches vertex F of the second, vertex B of the first matches vertex D of the second, and vertex C of the first matches vertex E of the second.
. This means that vertex A of the first triangle matches vertex F of the second, vertex B of the first matches vertex D of the second, and vertex C of the first matches vertex E of the second.
Since congruent means the triangles have the same size and shape, it implies that six pairs of corresponding parts have the same measure, the three angle-pairs and the three side-pairs. Thus, ![]() implies the following six facts,
implies the following six facts,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
and if all six of these are true, then the triangles are congruent.
Side-Angle-Side Postulate
Now it turns out that it is not necessary to establish that all six congruences are true for two given triangles in order to prove the triangles are congruent. It is enough to establish three of them, provided the right three are chosen. There are 4 such choices, and these are given the names SAS, SSS, ASA, and SAA (or AAS). One of them must be taken as a postulate, but then the other three can be proved (though the proofs can be tricky).
Usually SAS is the one that is taken as a postulate since it is the "most obvious." What it says is, if you have two triangles, a side of one is congruent to a side of the other (this is the first S), an angle on that side of one is congruent to an angle on that side of the other (this is the A), and the second side of the angle on one is congruent to the second side on that angle of the other (this is the final S), then the two triangles must be congruent (so their other sides and angles are congruent). By the way, SAS is not the same as SSA or ASS, which imply the angles are not between the congruent sides, and therefore do not imply the two triangles are congruent. SAS can be diagramed by marking the corresponding congruences with like marks:
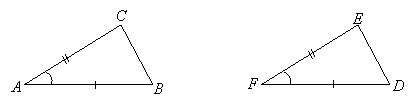
|
In this case, the known congruences are: |
|
|
|
|
|
|
|
If these three are valid, then the two triangles are congruent: ![]() .
.
Angle-Side-Side Doesn't Work
If the congruent angles are not included between the congruent sides, then we have SSA or ASS. These do not imply the two triangles are congruent, as the following illustrates:
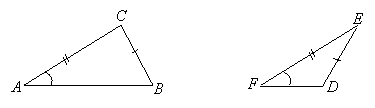
In this case, ![]() ,
, ![]() , and
, and ![]() , yet the triangles are clearly not congruent since they have different shapes.
, yet the triangles are clearly not congruent since they have different shapes.
Side-Side-Side Theorem
From the SAS postulate, two similar results (theorems) follow:
SSSIf we pair up the sides of two triangles and the sides of these pairs are congruent, then the two triangles are congruent:
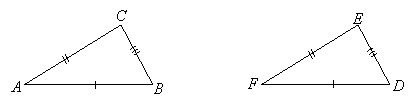
Here we have: ![]() ,
, ![]() ,
, ![]()
It follows from SSS that ![]() .
.
Angle-Side-Angle Theorem
ASAIf two angles of one triangle are congruent to two angles of another and the included sides are congruent, then the triangles are congruent:
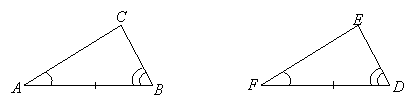
Here we have: ![]() ,
, ![]() ,
, ![]() .
.
It follows by ASA that ![]() .
.
Euclid's Proof of the ASA Theorem
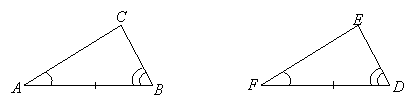 SSS and ASA follow logically from SAS. Here we will give Euclid's proof of one of them, ASA. It involves indirect reasoning to arrive at the conclusion that
SSS and ASA follow logically from SAS. Here we will give Euclid's proof of one of them, ASA. It involves indirect reasoning to arrive at the conclusion that ![]() must equal
must equal ![]() in the diagram, from which it follows (from SAS) that the triangles are congruent:
in the diagram, from which it follows (from SAS) that the triangles are congruent:
Theorem: If (see the diagram) ![]() ,
, ![]() , and
, and ![]() ,
,
then ![]() .
.
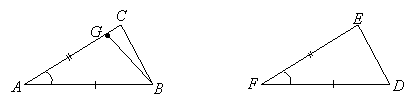 Proof: Suppose
Proof: Suppose ![]() and
and ![]() , and suppose
, and suppose ![]() is not equal to
is not equal to ![]() . Then one of these segments is longer than the other. Without loss of generality, we can suppose the longer segment is
. Then one of these segments is longer than the other. Without loss of generality, we can suppose the longer segment is ![]() (because otherwise we could just relabel everything). We can then choose a point G on
(because otherwise we could just relabel everything). We can then choose a point G on ![]() for which
for which ![]() , and then construct segment
, and then construct segment ![]() :
:
By SAS it then follows that ![]() . This implies that
. This implies that ![]() since these are corresponding parts of the congruent triangles. But
since these are corresponding parts of the congruent triangles. But ![]() is part of
is part of ![]() , and therefore smaller than it, and so
, and therefore smaller than it, and so ![]() (which is the same size as
(which is the same size as ![]() ) is smaller than
) is smaller than ![]() .
.
So if ![]() then
then ![]() . The contrapositive of this says, if
. The contrapositive of this says, if ![]() then
then ![]() . Therefore, if we have the three givens of our theorem (if
. Therefore, if we have the three givens of our theorem (if ![]() ,
, ![]() , and
, and ![]() ), then we also have
), then we also have ![]() , and so by SAS it follows that
, and so by SAS it follows that ![]() .
.
Side-Angle-Angle Theorem
The fourth result (theorem) follows from ASA and the fact that the angles of a triangle add to ![]() (which will be proved later using the parallel postulate):
(which will be proved later using the parallel postulate):
SAA
If two angles of one triangle are congruent to two angles of another and a side of the first triangle that is not common to both angles is congruent to a side of the second triangle that is not common to both angles, then the triangles are congruent:
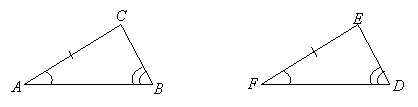
If ![]() ,
, ![]() , and
, and ![]() , it follows by SAA that
, it follows by SAA that ![]() .
.
Isosceles Triangle Theorem
Another result about triangles that is important and follows directly from SAS is the Isosceles Triangle Theorem. An isosceles triangle is one that has two equal sides. The Isosceles Triangle Theorem says that the angles opposite those sides will also be equal:
|
If
|
|
Its converse is also true: If two angles of a triangle are equal, then so are the sides opposite them. That is, if ![]() , then
, then ![]() .
.
Both of these results are almost obvious because an isosceles triangle is symmetric about a line splitting it in half:
Click here to return to the main Lesson 9 page.