Side-Angle-Side Postulate

Now it turns out that it is not necessary to establish that all six congruences are true for two given triangles in order to prove the triangles are congruent.  It is enough to establish three of them, provided the right three are chosen.  There are 4 such choices, and these are given the names SAS, SSS, ASA, and SAA (or AAS).  One of them must be taken as a postulate, but then the other three can be proved (though the proofs can be tricky). 

Usually SAS is the one that is taken as a postulate since it is the "most obvious."  What it says is, if you have two triangles, a side of one is congruent to a side of the other (this is the first S), an angle on that side of one is congruent to an angle on that side of the other (this is the A), and the second side of the angle on one is congruent to the second side on that angle of the other (this is the final S), then the two triangles must be congruent (so their other sides and angles are congruent).  By the way, SAS is not the same as SSA or ASS, which imply the angles are not between the congruent sides, and therefore do not imply the two triangles are congruent.  SAS can be diagramed by marking the corresponding congruences with like marks:

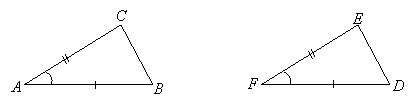
In this case, the known congruences are:	S:
	A:
	S:

If these three are valid, then the two triangles are congruent: .

 

toc | return to top | previous page | next page