Problem 1:

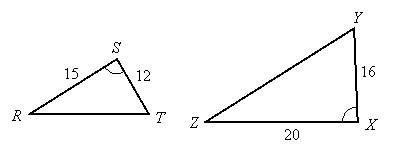
Solution: 

It appears that they are similar by SAS similarity, but we must check to see if ratios of the sides including the congruent angles are equal:

Ratio of shorter sides: 

Ratio of longer sides:  

Since the ratios reduce to the same fraction, the triangles are similar.

Problem 2: 

Are these triangles similar?

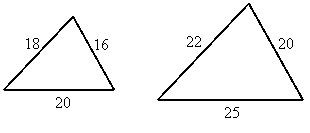
Solution: 

It looks like they might be similar by SSS similarity, but we must check the ratios:

Ratio of shortest sides: 

Ratio of longest sides:   

Ratio of other sides:     

These triangles are not similar since the third ratio is different from the other two.

Problem 3: 

Find the length of the side marked x: 

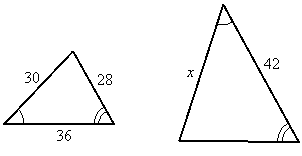
Solution: 

These triangles are similar by AA similarity.  Since x is the side opposite the doubly-marked angle, it corresponds to the side of length 30 in the triangle on the left.  The 42 corresponds to the side of length 36 in the triangle on the left, since both sides are opposite the unmarked angle. Therefore we can set up the following proportion to find x:

First we reduce the fraction on the right, and then we cross-multiply:

Problem 4: 

Jon is 6 feet tall.  At 3 PM he casts a shadow that is 4 feet long, and a pole out front of his house casts a shadow that is 32 feet long. How tall is the pole?

Solution:

Draw triangles to represent this situation: 

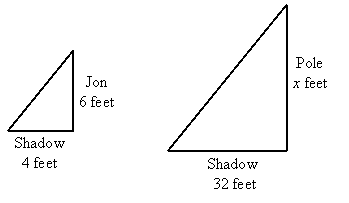
These are both right triangles, and since the sun makes the same angles at the shadow, they are similar by AA similarity.  Therefore we can set up a proportion and solve:

The pole is 48 feet tall.

toc | return to top | previous page