.SSS and SAS similarity
SSS Similarity
Two geometric figures are similar if one is a scaled version of the other. As a consequence, their angles will be the same. This includes triangles, and the scaling factor can be thought of as a ratio of side-lengths.
For example, triangle DEF is a scaled version of triangle ABC with a scaling factor of 1.5 (or 3/2), and we can write .
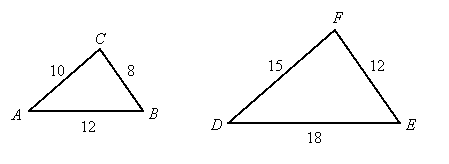
Notice that DE = 1.5AB, EF = 1.5BC, and DF = 1.5AC. If we form ratios of corresponding sides, we have:
, 
, and 
That is, the ratios of corresponding sides all reduce to the same fraction. We could form the reciprocals of the ratios, and they too will be the same:
, 
, and 
This is what we call "SSS similarity." That is, if ratios of three pairs of corresponding sides of two triangles are equal, then the triangles are similar. That common ratio is either the scaling factor or the reciprocal of the scaling factor, depending on the direction in which we do the scaling.
Example: Are these triangles similar? If so, write the similarity.
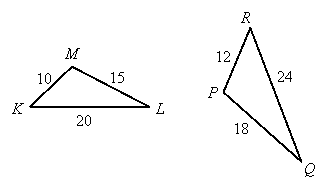
Solution:
To determine which sides "correspond," we list them from smallest to largest:
Ratio of smallest sides: 
Ratio of middle sides: 
Ratio of largest sides: 
Since these ratios are all equal, the triangles are similar by SSS similarity. To write the similarity, we make sure the triangles are named with the smallest side as the first two letters and the largest with the 2nd and 3rd letters:
Proportions Within Each Figure
In algebra, you can cross-multiply in a proportion such as 
, getting ad = bc. Another proportion that gives the same cross-product is 
. When interpreted for similar triangles, this shows that if you take the ratio of two sides in one triangle and the ratio of the two corresponding sides in the other, then these ratios will be the same.
For example, 
and the following ratios are all equal:
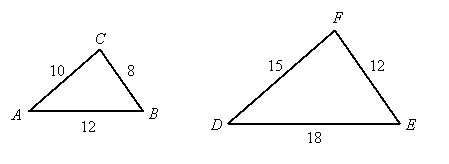
In other words, 
.
This is another way to express SSS similarity. That is, if all three corresponding ratios are the same, then the triangles are similar.
SAS Similarity
If two triangles have a common angle and the ratios of the sides that include this angle are equal, then the triangles are similar by SAS similarity.
Theorem:
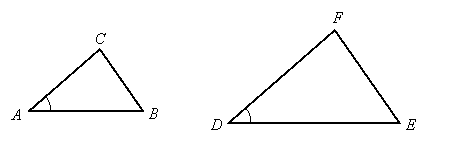
This theorem can be proved from AA similarity by embedding a triangle in the larger triangle that is congruent to the smaller triangle. Thus suppose triangle DEF is the larger triangle. Draw segment PQ so that DQ = AB and segment PQ is parallel to side FE. Then angle DQP is congruent to angle E since they are corresponding angles for the parallel lines, so triangles DQP and DEF are similar by AA similarity.
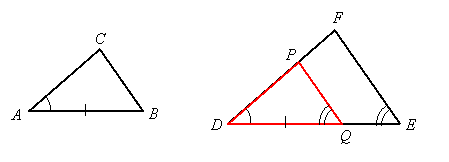
This gives us the proportion, 
. But we located point Q so that DQ = AB. Substituting this changes the proportion to: 
. But we also know (from the hypothesis of what we are trying to prove) that 
. Therefore, 
, so DP = AC. Thus triangle DQP is congruent to triangle ABC by the SAS congruence postulate. Since triangles DQP and DEF are similar, it therefore follows that triangles ABC and DEF are similar (this is a transitive property applied to congruent and similar triangles).
Sample Problems
We have three ways to establish that two triangle are similar: AA similarity, SSS similarity, and SAS similarity. The following problems illustrate these ideas.
Problem 1:
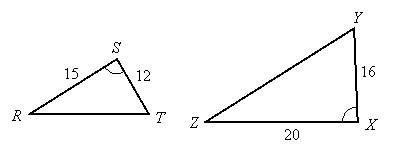
Solution:
It appears that they are similar by SAS similarity, but we must check to see if ratios of the sides including the congruent angles are equal:
Ratio of shorter sides: 
Ratio of longer sides: 
Since the ratios reduce to the same fraction, the triangles are similar.
Problem 2:
Are these triangles similar?
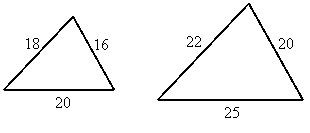
Solution:
It looks like they might be similar by SSS similarity, but we must check the ratios:
Ratio of shortest sides: 
Ratio of longest sides: 
Ratio of other sides: 
These triangles are not similar since the third ratio is different from the other two.
Problem 3:
Find the length of the side marked x:
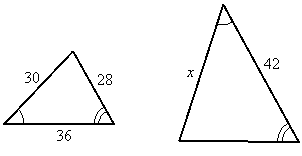
Solution:
These triangles are similar by AA similarity. Since x is the side opposite the doubly-marked angle, it corresponds to the side of length 30 in the triangle on the left. The 42 corresponds to the side of length 36 in the triangle on the left, since both sides are opposite the unmarked angle. Therefore we can set up the following proportion to find x:
First we reduce the fraction on the right, and then we cross-multiply:
Problem 4:
Jon is 6 feet tall. At 3 PM he casts a shadow that is 4 feet long, and a pole out front of his house casts a shadow that is 32 feet long. How tall is the pole?
Solution:
Draw triangles to represent this situation:
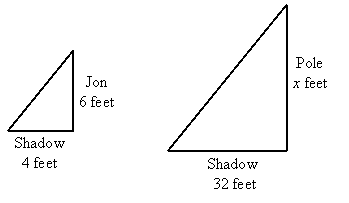
These are both right triangles, and since the sun makes the same angles at the shadow, they are similar by AA similarity. Therefore we can set up a proportion and solve:
The pole is 48 feet tall.