- Next
- Page 1 of 4
SSS Similarity
Two geometric figures are similar if one is a scaled version of the other. As a consequence, their angles will be the same. This includes triangles, and the scaling factor can be thought of as a ratio of side-lengths.
For example, triangle DEF is a scaled version of triangle ABC with a scaling factor of 1.5 (or 3/2), and we can write ![]() .
.
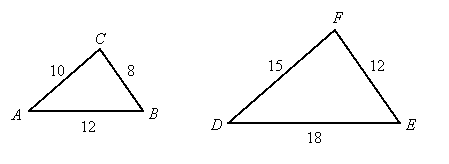
Notice that DE = 1.5AB, EF = 1.5BC, and DF = 1.5AC. If we form ratios of corresponding sides, we have:
![]() ,
, ![]() , and
, and ![]()
That is, the ratios of corresponding sides all reduce to the same fraction. We could form the reciprocals of the ratios, and they too will be the same:
![]() ,
, ![]() , and
, and ![]()
This is what we call "SSS similarity." That is, if ratios of three pairs of corresponding sides of two triangles are equal, then the triangles are similar. That common ratio is either the scaling factor or the reciprocal of the scaling factor, depending on the direction in which we do the scaling.
Example: Are these triangles similar? If so, write the similarity.
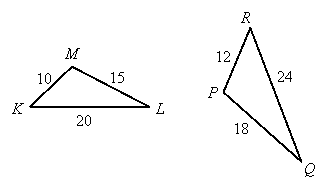
Solution:
To determine which sides "correspond," we list them from smallest to largest:
Ratio of smallest sides: ![]()
Ratio of middle sides: ![]()
Ratio of largest sides: ![]()
Since these ratios are all equal, the triangles are similar by SSS similarity. To write the similarity, we make sure the triangles are named with the smallest side as the first two letters and the largest with the 2nd and 3rd letters:
![]()