Theorem:

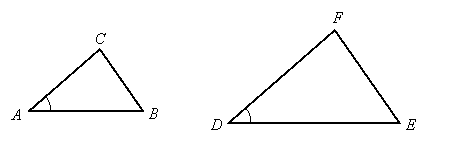
This theorem can be proved from AA similarity by embedding a triangle in the larger triangle that is congruent to the smaller triangle. Thus suppose triangle DEF is the larger triangle.  Draw segment PQ so that DQ = AB and segment PQ is parallel to side FE.  Then angle DQP is congruent to angle E since they are corresponding angles for the parallel lines, so triangles DQP and DEF are similar by AA similarity.

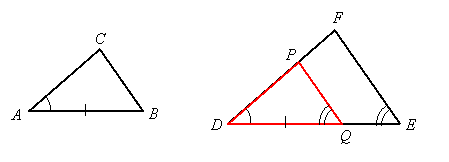
This gives us the proportion, .  But we located point Q so that DQ = AB.  Substituting this changes the proportion to:  . But we also know (from the hypothesis of what we are trying to prove) that .  Therefore, , so DP = AC.  Thus triangle DQP is congruent to triangle ABC by the SAS congruence postulate.  Since triangles DQP and DEF are similar, it therefore follows that triangles ABC and DEF are similar (this is a transitive property applied to congruent and similar triangles).