The Pythagorean Theorem is used frequently in construction and surveying.  It is the key to finding lengths of sides of objects that can be partitioned into right triangles.  Here are some examples of its use:

EXAMPLE 3:

How long is a diagonal of a rectangle that measures 5 cm by 12 cm?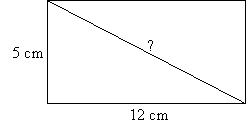

 SOLUTION:      

The diagonal cuts the rectangle into two right triangles.  Considering one of those triangles, the diagonal is the hypotenuse so we call its length c, and a = 5, b = 12.  Using the Pythagorean Theorem:  , so . 

The diagonal is 13 cm in length.

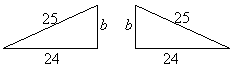
EXAMPLE 4:

The rafters of a slanting roof are 25 feet long, and the span from end-to-end is 48 feet. How high above the horizontal beams is the peak of  the roof?

SOLUTION:       If you place a segment from the peak of the roof perpendicular to a beam, you get two right triangles.  For one of these triangles the hypotenuse is 25 feet (so c = 25), and a leg is 24 ft (a = 24).  The unknown height is b, so use the Pythagorean Theorem to find it:   ,  ,   ,   .  So the peak of the roof is 7 ft above the beams.