Right Triangles
Altitudes
An altitude of any triangle is a segment that extends from a vertex to the opposite side (or an extension of the opposite side) and is perpendicular to that side. The dashed segments, ![]() , in the following figures are altitudes of the triangles:
, in the following figures are altitudes of the triangles:
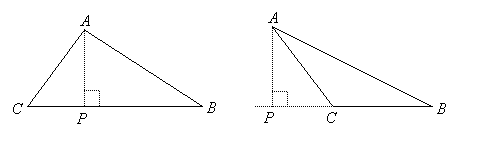
In the special case of a right triangle, each leg is an altitude perpendicular to the other leg, and there is a third altitude from the right angle perpendicular to the hypotenuse that plays an important role in measurement
|
Triangle ABC is a right triangle with hypotenuse
|
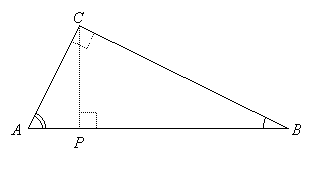 |

Three Similar Right Triangles
The altitude to the hypotenuse forms three similar triangles:

Notice that the similarities must be named consistently. In the above, the letters are in the order of double-marked angle, right angle, single-marked angle.
These similarities lead to important proportions, which can be more easily represented if we label the sides of the triangles: In ![]() , let a be the length of the side opposite angle A, b be the length of the side opposite angle B, and c be the length of the hypotenuse. Then in
, let a be the length of the side opposite angle A, b be the length of the side opposite angle B, and c be the length of the hypotenuse. Then in ![]() , b is the length of the hypotenuse; let d be the length of
, b is the length of the hypotenuse; let d be the length of ![]() and h the length of
and h the length of ![]() , which is the altitude of
, which is the altitude of ![]() . In
. In ![]() , the length of the hypotenuse is a and the length of
, the length of the hypotenuse is a and the length of ![]() is h; let e be the length of
is h; let e be the length of ![]() . Notice that d + e = c.
. Notice that d + e = c.
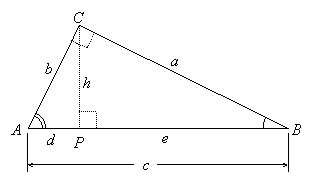
As an example, consider ![]() . If we consider the hypotenuse and short leg of each, the following ratios of corresponding parts are equal:
. If we consider the hypotenuse and short leg of each, the following ratios of corresponding parts are equal: ![]() . If we cross-multiply, we get
. If we cross-multiply, we get ![]() . This says the product of the hypotenuse and the altitude of a right triangle (in this case,
. This says the product of the hypotenuse and the altitude of a right triangle (in this case, ![]() ) is equal to the product of its legs.
) is equal to the product of its legs.

Forming Ratios
In some cases the same length may be used in two ratios, because it is common to the two similar triangles being considered.
| For example, in |
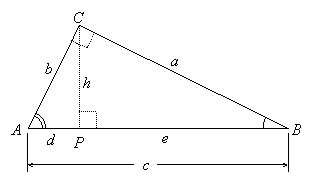 |
There are actually three geometric means that come from the above diagram:
|
Similar Triangles |
Proportion |
Geometric Mean |
|
|
|
|
|
|
|
|
|
|
|
|

Examples
Here are a couple of examples to show how these similarities can be used:
| EXAMPLE 1: | Find x: | 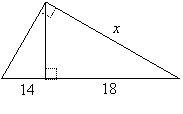 |
SOLUTION: x is the long leg of the whole triangle and the hypotenuse of the triangle on the right. So we use the ratio ![]() for both. Notice that the length of the hypotenuse of the whole triangle is 14 + 18 = 32. Thus,
for both. Notice that the length of the hypotenuse of the whole triangle is 14 + 18 = 32. Thus, ![]() . Cross-multiplying gives
. Cross-multiplying gives ![]() . Taking the square root,
. Taking the square root, ![]() .
.
| EXAMPLE 2: | Find x: | 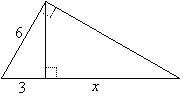 |
SOLUTION:
Since x is part of the triangle on the right only and there are no given parts of this triangle, it is easier to find the hypotenuse of the whole triangle, and then subtract 3 to get x. Thus we find y first:
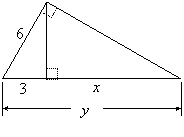
Considering the whole triangle and the triangle on the left, we can use the ratio ![]() for both:
for both: ![]() . Cross-multiplying gives
. Cross-multiplying gives ![]() , so
, so ![]() , and therefore
, and therefore ![]() .
.

The Pythagorean Theorem
As we learned in Unit 1, one of the most important theorems in geometry is the Pythagorean Theorem, named after the Greek mathematician Pythagoras who led in the discovery of its proof around 500 BC. This theorem gives a useful relationship between the three sides of any right triangle, and thus tells how to find a missing side when two of the sides are known.
|
Suppose in
|
|
In Pythagoras' time this important theorem was understood in terms of areas. In Unit 1 we learned that if you construct squares on the three sides of a right triangle, then the areas of the two squares on the legs add to the area of the square on the hypotenuse:
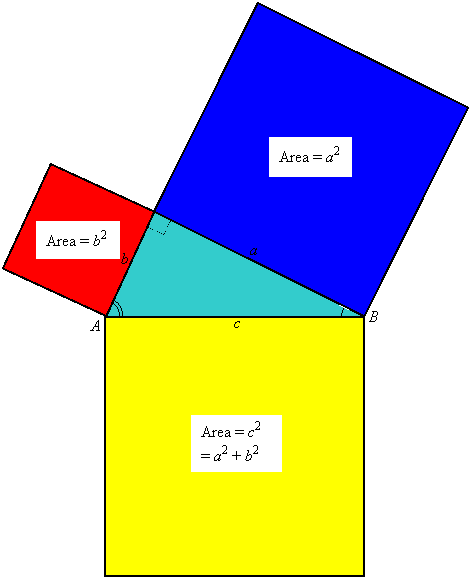

The Pythagorean Theorem is used frequently in construction and surveying. It is the key to finding lengths of sides of objects that can be partitioned into right triangles. Here are some examples of its use:
| EXAMPLE 3: | How long is a diagonal of a rectangle that measures 5 cm by 12 cm? | 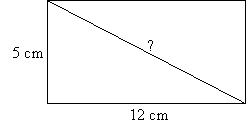 |
SOLUTION:
The diagonal cuts the rectangle into two right triangles. Considering one of those triangles, the diagonal is the hypotenuse so we call its length c, and a = 5, b = 12. Using the Pythagorean Theorem: ![]() , so
, so ![]() .
.
The diagonal is 13 cm in length.
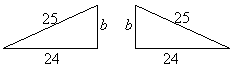
| EXAMPLE 4: | The rafters of a slanting roof are 25 feet long, and the span from end-to-end is 48 feet. How high above the horizontal beams is the peak of the roof? |  |
SOLUTION: If you place a segment from the peak of the roof perpendicular to a beam, you get two right triangles. For one of these triangles the hypotenuse is 25 feet (so c = 25), and a leg is 24 ft (a = 24). The unknown height is b, so use the Pythagorean Theorem to find it: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . So the peak of the roof is 7 ft above the beams.
. So the peak of the roof is 7 ft above the beams.