Three Similar Right Triangles
The altitude to the hypotenuse forms three similar triangles:

Notice that the similarities must be named consistently. In the above, the letters are in the order of double-marked angle, right angle, single-marked angle.
These similarities lead to important proportions, which can be more easily represented if we label the sides of the triangles: In ![]() , let a be the length of the side opposite angle A, b be the length of the side opposite angle B, and c be the length of the hypotenuse. Then in
, let a be the length of the side opposite angle A, b be the length of the side opposite angle B, and c be the length of the hypotenuse. Then in ![]() , b is the length of the hypotenuse; let d be the length of
, b is the length of the hypotenuse; let d be the length of ![]() and h the length of
and h the length of ![]() , which is the altitude of
, which is the altitude of ![]() . In
. In ![]() , the length of the hypotenuse is a and the length of
, the length of the hypotenuse is a and the length of ![]() is h; let e be the length of
is h; let e be the length of ![]() . Notice that d + e = c.
. Notice that d + e = c.
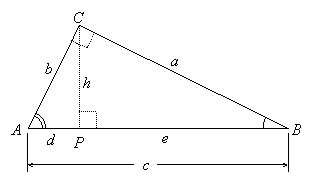
As an example, consider ![]() . If we consider the hypotenuse and short leg of each, the following ratios of corresponding parts are equal:
. If we consider the hypotenuse and short leg of each, the following ratios of corresponding parts are equal: ![]() . If we cross-multiply, we get
. If we cross-multiply, we get ![]() . This says the product of the hypotenuse and the altitude of a right triangle (in this case,
. This says the product of the hypotenuse and the altitude of a right triangle (in this case, ![]() ) is equal to the product of its legs.
) is equal to the product of its legs.