The Pythagorean Theorem
As we learned in Lesson 4, one of the most important theorems in geometry is the Pythagorean Theorem, named after the Greek mathematician Pythagoras who led in the discovery of its proof around 500 BC. This theorem gives a useful relationship between the three sides of any right triangle, and thus tells how to find a missing side when two of the sides are known.
|
Suppose in
|
|
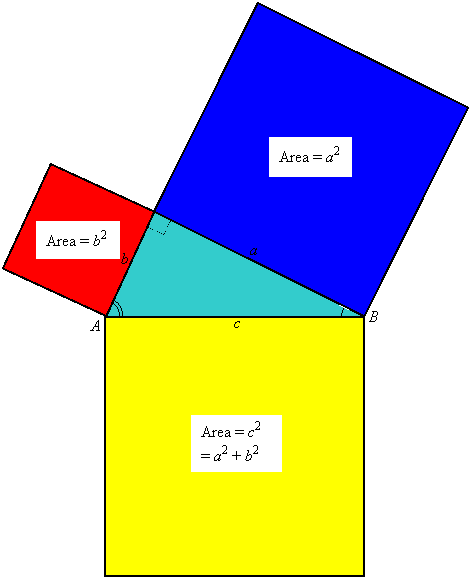
In Pythagoras' time this important theorem was understood in terms of areas. In Unit 1 we learned that if you construct squares on the three sides of a right triangle, then the areas of the two squares on the legs add to the area of the square on the hypotenuse:
Content ©2008. All Rights Reserved.
Date last modified: August 6, 2008.
the legs are 
and 
, and the hypotenuse is 
. As before, let 
, 
, and 
. We can relate these three lengths by considering the altitude h to the hypotenuse. This altitude splits the hypotenuse into two segments of lengths d and e, where d + e = c, and by the previous results we know that a is the geometric mean of e and c (so 
), and b is the geometric mean of d and c (so 
). If we add these, we have 
. But we can factor out c on the right, so 
and since e + d = c, this gives 
. That's the Pythagorean Theorem.