From the Triangle Midsegment Theorem it follows that a segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length, since there can be only one line through a given point (the midpoint of one side) parallel to another line (the third side).

Another way to state the Triangle Midsegment Theorem is:

If an angle is cut by two parallel lines so that the pairs of segments on one side of the angle are equal, then the pairs of segments on the other side of the angle will be equal and  the segment on the parallel between the vertex of the angle and the other parallel is half as long as the segment on the other parallel: 

This result can be repeated as in the following example:

Problem:     Suppose parallel lines l, m, n, and p cut  so that segments , , , and  all have the same length:

If AP = 8 and EQ = 28, then how long are  and ?

Solution:     Lines l and m cut the angle as in the Triangle Midsegment Theorem, so we know the following lengths, where for the time being we call BP x: 

Lines m and p also cut the angle as in the Triangle Midsegment Theorem, so we know these lengths:

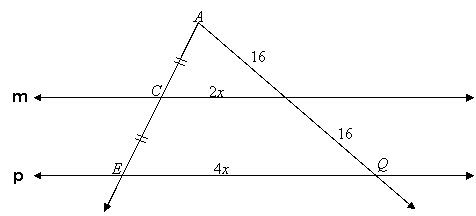
Now we can see that AQ = 32.  Since P is between A and Q, AP + PQ = AQ, which tells us PQ = 24.  Also, EQ = 27, and this is 4x, so x = 7:  AP = 7.