Proof of the Triangle Midsegment Theorem
To shorten proofs in geometry, we can sometimes prove preliminary results. In the case of the Triangle Midsegment Theorem, a preliminary result is that opposite sides of a parallelogram are congruent. Recall that a parallelogram is a quadrilateral with opposite sides congruent. So first we will prove:
Theorem: The opposite sides of a parallelogram are congruent.
Proof:
|
Let the parallelogram be ABCD, and draw the diagonal |
 |
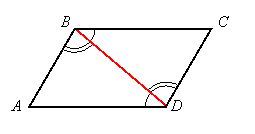Now we can prove the Triangle Midsegment Theorem:
| Given: | M is the midpoint of  , N is on  , and  |
 |
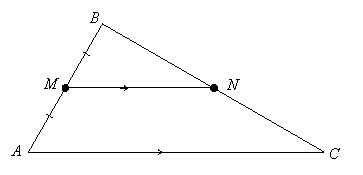| Prove: | N is the midpoint of  and  |
|
Proof:
We will show that the result follows by proving two triangles congruent. First locate point P on side 
so 
, and construct segment 
:
Notice that 
is a transversal for parallel segments 
and 
, so the corresponding angles, 
and 
are congruent:
Now, for 
and 
we have:
(because M is the midpoint of 
)
and 
Therefore, these triangles are congruent by the SAS postulate, and so their other corresponding parts are congruent: 
, 
, and 
. Also, since 
(this was given), 
because these are corresponding angles for the transversal 
. Therefore, 
. But these are corresponding angles for segments 
and 
with transversal 
, so by the Corresponding Angle Theorem, 
. Thus, MNCP is a parallelogram, and by Example 3 from the previous lesson, its opposite sides are equal:
and 
:
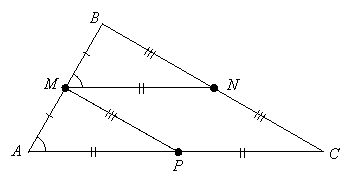
Since BN and NC are both equal to MP, they are equal to each other, so N is the midpoint of 
. Likewise, since AP and PC are both equal to MN, P is the
midpoint of 
:
But AP = MN
Therefore 
Content ©2008. All Rights Reserved.
Date last modified: August 5, 2008.
. Then since opposite sides are parallel (this is the definition of a parallelogram), 
and 
since these are alternate interior angles for the parallel sides with transversal 
. Thus 
by ASA since they have side 
in common. Therefore 
and 
since these are corresponding parts of the congruent triangles.