Overlapping Triangles

When triangles overlap, you have to imagine them separately.  The following problems illustrate this idea. 

Problem 1:

Given:   and  are right angles, , and

Prove:   is isosceles

 

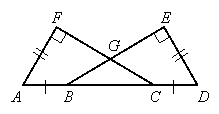
Proof:

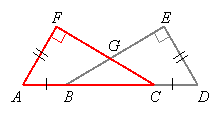
The overlapping triangles are  and .  We will first show they are congruent.

Concentrating on , since  is between  and , .

Likewise for ,

 

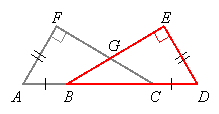
Since , which says , we can substitute  for  in  to get .  Now we have two equations with the same left sides:

 and

Therefore the right sides are equal:  , so .  We also know  and  and  are right angles, so it follows that  by HL.  So  because these are corresponding parts of the congruent triangles.  They are also angles of , so by the isosceles triangle theorem, this is an isosceles triangle with .

 Problem 2:

Given:  , and

Prove: 

 

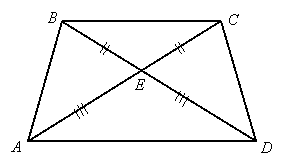
Proof:

We have overlapping triangles  and : 

  

 

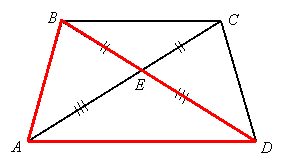
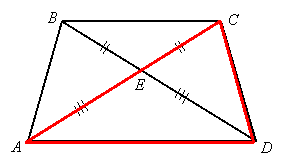
By segment addition,  and .  Since  and , we can substitute lengths to conclude that , or .  Now  is isosceles, so by the isosceles triangle theorem, .  We also have a common side, .  Therefore  by SSS, so  since they are corresponding parts of the congruent triangles.

toc | return to top | previous page