Perpendicular Bisector of a Chord
A chord of a circle is a segment whose endpoints are on the circle:
Theorem:
The perpendicular bisector of a chord of a circle passes through the center of the circle.
Proof:
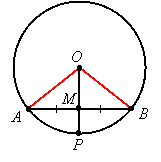
Let the center of the circle be labeled as 
, the endpoints of the chord as 
and 
, 
the midpoint of 
, and 
the point where 
intersects the circle. Then all we have to prove is that 
.
since each is a radius of the circle. Since 
(
is the midpoint of 
) and 
, 
by SSS. Because they are corresponding parts of these congruent triangles, 
, so their measures are equal. But these angles are a linear pair, so their measures add to 180o: 
. Substituting 
for 
, we have 
, so 
. Therefore 
, which makes 
the perpendicular bisector of 
.
Content ©2008. All Rights Reserved.
Date last modified: August 4, 2008.