Angle Inscribed in a Semicircle
Theorem: An angle inscribed in a semicircle is a right angle.
That is, if 
and 
are endpoints of a diameter of a circle with center 
, and 
is a point on the circle, then 
is a right angle.
Proof:
Draw line 
. This is a radius of the circle, as are 
and 
, so 
. Label the following angle measures: 
and 
:
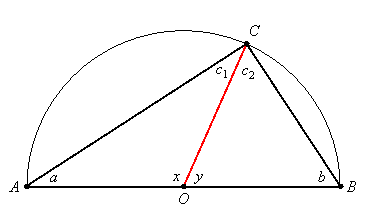
By the isosceles triangle theorem (applied to triangles AOC and BOC), c1 = a and c2 = b. The sum of the angles in any triangle is 180o, so a + c1 + x = 180o and b + c2 + y = 180o. Substituting c1 for a and c2 for b, this gives: 2c1 + x = 180o and 2c2 + y = 180o. If we add these two equations, we have: 2c1 + 2c2 + x + y = 360o. But x + y = 180o since 
and 
are a linear pair. Substituting 180o for x + y gives us 2c1 + 2c2 + 180o = 360o. Subtracting 180o from both sides and dividing by 2 gives: c1 + c2 = 90o. But 
, so 
is a right angle.
Content ©2008. All Rights Reserved.
Date last modified: August 4, 2008.