Proofs involving Measurements
Review of Addition Postulates
Many results in geometry depend on lengths of segments or measures of angles. Sometimes the segment addition or angle addition postulates play an important role, so we will state them once again:
Segment Addition Postulate
If P is between A and B, then AP + BP = AB, and conversely.
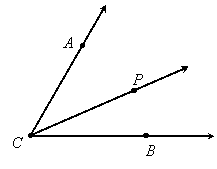
Angle Addition Postulate
If 
is interior to 
then 
, and conversely.
Angle Inscribed in a Semicircle
Theorem: An angle inscribed in a semicircle is a right angle.
That is, if 
and 
are endpoints of a diameter of a circle with center 
, and 
is a point on the circle, then 
is a right angle.
Proof:
Draw line 
. This is a radius of the circle, as are 
and 
, so 
. Label the following angle measures: 
and 
:
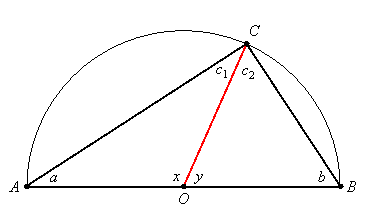
By the isosceles triangle theorem (applied to triangles AOC and BOC), c1 = a and c2 = b. The sum of the angles in any triangle is 180o, so a + c1 + x = 180o and b + c2 + y = 180o. Substituting c1 for a and c2 for b, this gives: 2c1 + x = 180o and 2c2 + y = 180o. If we add these two equations, we have: 2c1 + 2c2 + x + y = 360o. But x + y = 180o since 
and 
are a linear pair. Substituting 180o for x + y gives us 2c1 + 2c2 + 180o = 360o. Subtracting 180o from both sides and dividing by 2 gives: c1 + c2 = 90o. But 
, so 
is a right angle.
Perpendicular Bisector of a Chord
A cord of a circle is a segment whose endpoints are on the circle:
Theorem:
The perpendicular bisector of a chord of a circle passes through the center of the circle.
Proof:
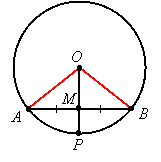
Let the center of the circle be labeled as 
, the endpoints of the chord as 
and 
, 
the midpoint of 
, and 
the point where 
intersects the circle. Then all we have to prove is that 
.
since each is a radius of the circle. Since 
(
is the midpoint of 
) and 
, 
by SSS. Because they are corresponding parts of these congruent triangles, 
, so their measures are equal. But these angles are a linear pair, so their measures add to 180o: 
. Substituting 
for 
, we have 
, so 
. Therefore 
, which makes 
the perpendicular bisector of 
.
Overlapping Triangles
When triangles overlap, you have to imagine them separately. The following problems illustrate this idea.
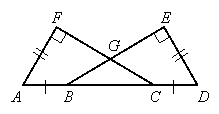
Problem 1:
Given: 
and 
are right angles, 
, and 
Prove: 
is isosceles
Proof:
The overlapping triangles are 
and 
. We will first show they are congruent.
Concentrating on 
, since 
is between 
and 
, 
.
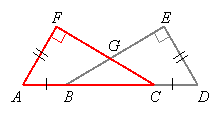
Likewise for 
, 
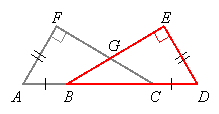
Since 
, which says 
, we can substitute 
for 
in 
to get 
. Now we have two equations with the same left sides:
and 
Therefore the right sides are equal: 
, so 
. We also know 
and 
and 
are right angles, so it follows that 
by HL. So 
because these are corresponding parts of the congruent triangles. They are also angles of 
, so by the isosceles triangle theorem, this is an isosceles triangle with 
.
Problem 2:
Given: 
, and 
Prove: 
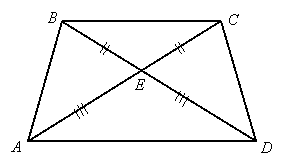
Proof:
We have overlapping triangles 
and 
:
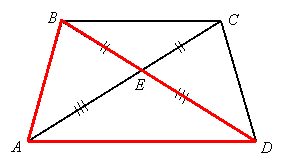
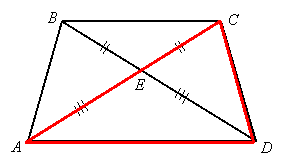
By segment addition, 
and 
. Since 
and 
, we can substitute lengths to conclude that 
, or 
. Now 
is isosceles, so by the isosceles triangle theorem, 
. We also have a common side, 
. Therefore 
by SSS, so 
since they are corresponding parts of the congruent triangles.