Pythagorean Triples and the Converse of the Pythagorean Theorem

When all three sides of a right triangle are whole numbers, the lengths are said to form a "Pythagorean triple." For example, the lengths 3, 4, and 5 are a Pythagorean triple. So are the lengths 5, 12, and 13.

Whenever the square of the largest of three numbers is equal to the sum of the squares of the other two, then those three numbers can be side-lengths of a right triangle. This is known as the "converse" of the Pythagorean Theorem. If those three numbers are whole numbers, then they are a Pythagorean triple.

There is an algebraic method for finding Pythagorean triples:

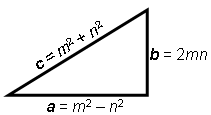Suppose the sides of a right triangle are labeled a, b, and c, where c is the hypotenuse. Choose two positive whole numbers, m and n, where m is bigger than n. Let a = m² − n² and let

c = m² + n². Then b² = c² − a² = (m² + n²)² − (m² − n²)². Using algebra, it can be seen that this simplifies to 4m²n², and so b = 2mn.

The following table shows some Pythagorean triples that result from various choices of the values of m and n:

toc | return to top | previous page