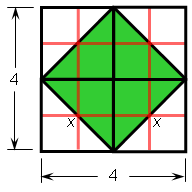
In Plato's dialog Meno, Socrates led a slave boy to construct a square with area of 8 square feet, starting with a square of area 4 square feet. The idea was to embed it at a 45o angle in a 4 foot by 4 foot square.Exact Value
Exact vs Approximate
In Plato's dialog Meno, Socrates led a slave boy to construct a square with area of 8 square feet, starting with a square of area 4 square feet. The idea was to embed it at a 45o angle in a 4 foot by 4 foot square.
The length of a side of the embedded square was never determined, though Socrates did make the slave discover it was not 4 feet. But we know the area of a square is its length times its width, so if x is the length (and therefore also the width), then x2 = 8, so x is the square root of 8. A calculator gives a decimal value as 2.828427125, but this is only as accurate to the number of places the calculator can display, and it is somewhat "ugly." In any case it is an approximate value of the side-length.
In geometry we prefer to keep the exact value since it is easier to write and allows the freedom to later compute answers to any desired degree of accuracy. It also helps us compare results. So instead of writing x = 2.828427125 or any similarly rounded-off value for the length of a side of our square, we simply write
This is the exact value of the side length.
When circles are involved, the formulas C = 2πr and A = πr2 give answers involving π. Like the square root of 8, π has a never-ending decimal representation and can only be approximated, so again we prefer to not use the approximate value and instead leave π in our answer. For example, the circumference of a circle of radius 2 feet is exactly 4π feet, but only approximately 12.57 feet.
Simplifying Square Roots
If the square root of a whole number is itself a whole number, then the original number is called a perfect square. For example, 16 is a perfect square because the square root of 16 is 4. Likewise, 49 is a perfect square because the square root of 49 is 7.
On the other hand, numbers like 8 and 2 are not perfect squares since their square roots are not whole numbers. In fact, when the square root of a whole number is not a whole number, then its decimal form never ends. Such square roots are called irrational numbers.
We can easily list the perfect squares in order by simply squaring the counting numbers. They are 1, 4, 9, 16, 25, 36, 49, 64, and so on.
Square roots of perfect squares can always be "simplified." Just take the square root.
Some irrational square roots can also be "simplified." For example, the square root of 8 is the side-length (in feet) of a square having area 8 square feet. Such a square can be made from 4 squares of area 2 square feet, and each of these smaller squares has a side length of square root of 2 feet. Therefore, the side length of the larger square must be twice this, so it must be true that
Rather than drawing pictures of squares to simplify irrational square roots, you can use the following procedure:
1. Find the largest perfect square that evenly divides the number under the square-root sign.
2. Use the fact that square roots multiply to simplify as the product of a whole number and an irrational square root.
For example, the largest perfect square that goes into 8 is 4, so we can simplify the square root of 8 as follows:
As another example, suppose we have to simplify the square root of 252. Click in the box below to see how this is done.
Squaring Square Roots
The square of a single square root is the number inside. For example:
This is because the square root of a number is another number whose square is the given number.
To square a product of a whole number and an irrational square root, you just multiply it by itself and then simplify. For example,
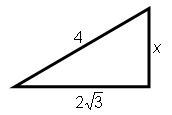This is sometimes necessary when finding a simplified exact length. For example, to find the exact value of x in the triangle on the right, you apply the Pythagorean Theorem and simplify:
Pythagorean Triples and the Converse of the Pythagorean Theorem
When all three sides of a right triangle are whole numbers, the lengths are said to form a "Pythagorean triple." For example, the lengths 3, 4, and 5 are a Pythagorean triple. So are the lengths 5, 12, and 13.
Whenever the square of the largest of three numbers is equal to the sum of the squares of the other two, then those three numbers can be side-lengths of a right triangle. This is known as the "converse" of the Pythagorean Theorem. If those three numbers are whole numbers, then they are a Pythagorean triple.
There is an algebraic method for finding Pythagorean triples:
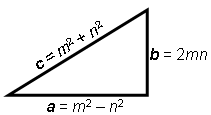Suppose the sides of a right triangle are labeled a, b, and c, where c is the hypotenuse. Choose two positive whole numbers, m and n, where m is bigger than n. Let a = m2 − n2 and let
c = m2 + n2. Then b2 = c2 − a2 = (m2 + n2)2 − (m2 − n2)2. Using algebra, it can be seen that this simplifies to 4m2n2, and so b = 2mn.
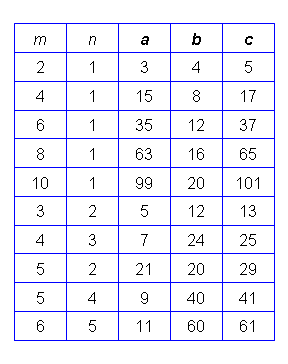
The following table shows some Pythagorean triples that result from various choices of the values of m and n:
Click here to return to the main Lesson 2 page.