Simplifying Square Roots

If the square root of a whole number is itself a whole number, then the original number is called a perfect square. For example, 16 is a perfect square because the square root of 16 is 4. Likewise, 49 is a perfect square because the square root of 49 is 7.

On the other hand, numbers like 8 and 2 are not perfect squares since their square roots are not whole numbers. In fact, when the square root of a whole number is not a whole number, then its decimal form never ends. Such square roots are called irrational numbers.

We can easily list the perfect squares in order by simply squaring the counting numbers. They are 1, 4, 9, 16, 25, 36, 49, 64, and so on.

Square roots of perfect squares can always be "simplified." Just take the square root.

Some irrational square roots can also be "simplified." For example, the square root of 8 is the side-length (in feet) of a square having area 8 square feet. Such a square can be made from 4 squares of area 2 square feet, and each of these smaller squares has a side length of square root of 2 feet. Therefore, the side length of the larger square must be twice this, so it must be true that

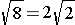
Rather than drawing pictures of squares to simplify irrational square roots, you can use the following procedure:

1. Find the largest perfect square that evenly divides the number under the square-root sign.

2. Use the fact that square roots multiply to simplify as the product of a whole number and an irrational square root.

For example, the largest perfect square that goes into 8 is 4, so we can simplify the square root of 8 as follows:

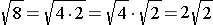
As another example, suppose we have to simplify the square root of 252. Click in the box below to see how this is done.

 

toc | return to top | previous page | next page