Exact vs Approximate

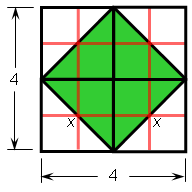In Plato's dialog Meno, Socrates led a slave boy to construct a square with area of 8 square feet, starting with a square of area 4 square feet. The idea was to embed it at a 45^o angle in a 4 foot by 4 foot square.

The length of a side of the embedded square was never determined, though Socrates did make the slave discover it was not 4 feet. But we know the area of a square is its length times its width, so if x is the length (and therefore also the width), then x² = 8, so x is the square root of 8. A calculator gives a decimal value as 2.828427125, but this is only as accurate to the number of places the calculator can display, and it is somewhat "ugly." In any case it is an approximate value of the side-length.

In geometry we prefer to keep the exact value since it is easier to write and allows the freedom to later compute answers to any desired degree of accuracy. It also helps us compare results. So instead of writing x =  2.828427125 or any similarly rounded-off value for the length of a side of our square, we simply write

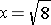
This is the exact value of the side length.

When circles are involved, the formulas C = 2πr and A = πr² give answers involving π. Like the square root of 8, π has a never-ending decimal representation and can only be approximated, so again we prefer to not use the approximate value and instead leave π in our answer. For example, the circumference of a circle of radius 2 feet is exactly 4π feet, but only approximately 12.57 feet.

 

toc | return to top | next page