Counterexamples and the Contrapositive

Counterexamples

The statement, “all birds fly” happens to be false. This is because there are some birds, like the penguin, that don’t fly at all.

To demonstrate (or “prove”) that a statement like this is false, all we need to do is supply an example that shows it is false. Such an example is called a counterexample. Penguin is a counterexample to “all birds fly.”

In general, a counterexample is any example that shows some statement is false.

The Contrapositive

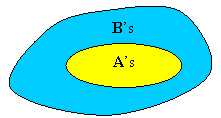image003.gif As discussed above, if-then statements are equivalent to all statements, and both can be represented by Venn diagrams. The statement, "all A’s are B’s" is diagrammed as:

 

 

 

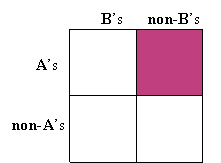image007.gif This shows that the A’s are a subset of the B’s. As a consequence, there are no A’s that are non-B’s (no part of the A-set is outside of the B-set). Another way to diagram this is to make a 2 by 2 table with the A’s and non-A’s as rows, and the B’s and non-B’s as columns. We darken the cell corresponding to A’s and non-B’s to indicate this cell is empty (there is no overlap):

 

If we look at the A row, the only cell containing elements (not darkened) is in the B column. This tells us that all A’s are B’s.

Likewise, if we look at the non-B column, the only cell containing elements is in the non-A row. From this we see that the following statement is also true:

All non-B’s are non-A’s.

In other words, the two statements "All A’s are B’s" and "All non-B’s are non-A’s" are equivalent.

In if-then form, these statements are equivalent:

If something is an A then it is a B       and       If something is not a B then it is not an A.

Equivalent statements like this are called contrapositives. To form the contrapositive of a conditional statement, you negate both the hypothesis and conclusion and switch them:

Statement:          If hypothesis then conclusion.

Contrapositive:  If not conclusion then not hypothesis.

Here’s a common-sense example:

Statement:         If it is raining then the streets are wet.

Contrapositive: If the streets are not wet then it is not raining.

Think about it. Both statements say the same thing, but in different ways.

toc | return to top | previous page | next page