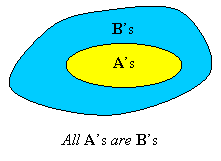
In the first case the A’s are contained in the B’s, while in the second case the B’s are contained in the A’s.

In if-then form, the statements

If it is an A then it is a B       and       If it is an B then it is an A

are just different statements. Each is called the converse of the other. The truth of one does not imply the truth of the other:

True: If a figure is a square then it has 4 equal sides.

False: If a figure has 4 equal sides then it is a square.

In some situations a statement and its converse are both true. In the case of “All A’s are B’s and all B’s are A’s” this would mean the A’s and B’s are exactly the same things, so we can only draw one set in our Venn diagram:

The shortened form of this statement is:

It is an A if and only if it is a B.

Such a statement is called a biconditional and is equivalent to:

If it is an A then it is a B and if it is a B then it is an A.

Sometimes we state it this way:

If it is an A then it is a B, and conversely.

The "and conversely" part means the converse is also true.

Definitions are sometimes stated in if-then form, but are really biconditionals since they must be reversible.

For example, we might define perpendicular this way:

If two lines are perpendicular then they intersect at right angles.

What we really mean is, perpendicular lines are lines that intersect at right angles.

Or we could be precise and say:

Two lines are perpendicular if and only if they intersect at right angles.

"If and only if" means both the statement and its converse are true.