But it is not a simple matter to define things. For example, we know that squares have 4 sides that are equal in length. But is that a good definition of a square? This figure has 4 sides that are the same length, but it isn't a square:Deductive Logic
Definitions
Geometry (and mathematics in general) is a very precise subject. Figures are classified according to certain properties, and definitions must be completely clear.
As in Plato’s dialog, Meno, we all have some notions of what certain figures are. For example, we know what a square is. However, some people might be misled by the way one is drawn. A baseball diamond is a square, but it is tilted at 45o when viewed from home base.
But it is not a simple matter to define things. For example, we know that squares have 4 sides that are equal in length. But is that a good definition of a square? This figure has 4 sides that are the same length, but it isn't a square:
The statement, “a square is a 4-sided figure whose sides have the same length” happens to be a true statement, but it cannot serve as a definition of a square since it is not “reversible.” That is, if the sides of a 4-sided figure have the same length then that figure might not be a square.
A square also has to have its sides perpendicular. In other words, the definition of a square must include all important properties that distinguish a square from other 4-sided figures:
Definition: A square is a 4-sided figure in which all sides are equal and pairs of sides are perpendicular.
We can state 4 properties a good definition must possess:
1. It names the term being defined.
2. It identifies the category to which the term belongs.
3. It states the properties that distinguish the term from others in that category.
4. It is reversible.
In our definition of a square these properties are:
1. Term: square
2. Category: 4-sided figures
3. Properties: equal sides, perpendicular sides
4. Reversible: No other 4-sided figures have those properties.
Conditional Statements
The statement, all squares have 4 equal sides happens to be true, though it cannot serve as the definition of a square. Another way to say this is, if a figure is a square then it has 4 equal sides. Such a statement (written in if-then form) is called a conditional statement. It consists of two parts: a statement between the words if and then, and a statement after the word then. The first part is called the hypothesis and the second the conclusion. Conditional statements always have the form:
If hypothesis then conclusion.
They are equivalent to “all” statements of this form:
All things that make the hypothesis true are things that make the conclusion true.
In this sense, the hypothesis and conclusion describe two categories or sets to which things belong, and both statements imply that the hypothesis category is contained in the conclusion category. This can be represented by a Venn diagram:
For example:
All A’s are B’s or If it is an A then it is a B
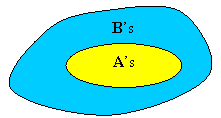both tell us that the A’s are a subset of the B’s:
The Converse and Biconditionals
The statements All A’s are B’s and All B’s are A’s say very different things, as can be seen from their Venn diagrams:
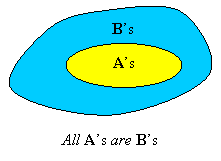
In the first case the A’s are contained in the B’s, while in the second case the B’s are contained in the A’s.
In if-then form, the statements
If it is an A then it is a B and If it is an B then it is an A
are just different statements. Each is called the converse of the other. The truth of one does not imply the truth of the other:
True: If a figure is a square then it has 4 equal sides.
False: If a figure has 4 equal sides then it is a square.
In some situations a statement and its converse are both true. In the case of “All A’s are B’s and all B’s are A’s” this would mean the A’s and B’s are exactly the same things, so we can only draw one set in our Venn diagram:
The shortened form of this statement is:
It is an A if and only if it is a B.
Such a statement is called a biconditional and is equivalent to:
If it is an A then it is a B and if it is a B then it is an A.
Sometimes we state it this way:
If it is an A then it is a B, and conversely.
The "and conversely" part means the converse is also true.
Definitions are sometimes stated in if-then form, but are really biconditionals since they must be reversible.
For example, we might define perpendicular this way:
If two lines are perpendicular then they intersect at right angles.
What we really mean is, perpendicular lines are lines that intersect at right angles.
Or we could be precise and say:
Two lines are perpendicular if and only if they intersect at right angles.
"If and only if" means both the statement and its converse are true.
Counterexamples and the Contrapositive
The statement, “all birds fly” happens to be false. This is because there are some birds, like the penguin, that don’t fly at all.
To demonstrate (or “prove”) that a statement like this is false, all we need to do is supply an example that shows it is false. Such an example is called a counterexample. Penguin is a counterexample to “all birds fly.”
In general, a counterexample is any example that shows some statement is false.
As discussed above, if-then statements are equivalent to all statements, and both can be represented by Venn diagrams. The statement, "all A’s are B’s" is diagrammed as:
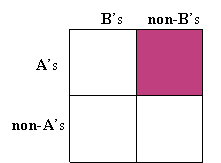This shows that the A’s are a subset of the B’s. As a consequence, there are no A’s that are non-B’s (no part of the A-set is outside of the B-set). Another way to diagram this is to make a 2 by 2 table with the A’s and non-A’s as rows, and the B’s and non-B’s as columns. We darken the cell corresponding to A’s and non-B’s to indicate this cell is empty (there is no overlap):
If we look at the A row, the only cell containing elements (not darkened) is in the B column. This tells us that all A’s are B’s.
Likewise, if we look at the non-B column, the only cell containing elements is in the non-A row. From this we see that the following statement is also true:
All non-B’s are non-A’s.
In other words, the two statements "All A’s are B’s" and "All non-B’s are non-A’s" are equivalent.
In if-then form, these statements are equivalent:
If something is an A then it is a B and If something is not a B then it is not an A.
Equivalent statements like this are called contrapositives. To form the contrapositive of a conditional statement, you negate both the hypothesis and conclusion and switch them:
Statement: If hypothesis then conclusion.
Contrapositive: If not conclusion then not hypothesis.
Here’s a common-sense example:
Statement: If it is raining then the streets are wet.
Contrapositive: If the streets are not wet then it is not raining.
Think about it. Both statements say the same thing, but in different ways.
Syllogisms
A syllogism is a logical argument in which a conclusion is reached based on some known facts which are usually stated in if-then or all form. This kind of logic played a central role in ancient Greek mathematics and is the essence of proof in mathematics today. Aristotle (around 350 BC) wrote extensively about logic and syllogisms, and this forms the basis of western culture.
Here is an example of a syllogism. If we know the following facts:
1. All teachers are in the library.
2. Everyone in the library is watching Dr. T’s lecture.
3. Ms. Jones is a teacher.
Then we can reach any of the following three conclusions:
(a) Ms. Jones is in the library.
(b) Ms. Jones is watching Dr. T’s lecture.
(c) All teachers are watching Dr. T’s lecture.
In other words, we just follow the string of statements in a common-sense way. However, we must be cautious in some cases. Many people confuse a statement with its converse. For example, if we also know this statement is true:
4. Mr. Smith is in the library.
then we can not conclude that Mr. Smith is a teacher. The first statement says all teachers are in the library, but it does not say that everyone in the library is a teacher.
Sometimes you have to use the contrapositive to reach a conclusion. The contrapositive is important to understand, because it is the basis of the logic used in certain proofs. Such proofs are called “indirect” since they rely not on the given form of a statement, but on its contrapositive.
The logic of an indirect proof is essentially this: If you want to prove B follows from A, try assuming B is not true and show that this leads to the conclusion that A is not true. Thus to prove “If A then B” you instead prove “If not B then not A,” which is equivalent.
Here is an example of the use of the contrapositive (or an indirect proof) to arrive at a conclusion. Suppose the following two facts are true:
1. Everyone in the library is watching Dr. T’s lecture.
2. Murphy is not watching Dr. T’s lecture.
We can conclude that Murphy is not in the library, because the first statement is equivalent to, “If someone is in the library then that person is watching Dr. T’s lecture,” and this in turn is equivalent to its contrapositive, “If someone is not watching Dr. T’s lecture then that person is not in the library.”