Conditional Statements

The statement, all squares have 4 equal sides happens to be true, though it cannot serve as the definition of a square. Another way to say this is, if a figure is a square then it has 4 equal sides. Such a statement (written in if-then form) is called a conditional statement. It consists of two parts: a statement between the words if and then, and a statement after the word then. The first part is called the hypothesis and the second the conclusion. Conditional statements always have the form:

If hypothesis then conclusion.

They are equivalent to “all” statements of this form:

All things that make the hypothesis true are things that make the conclusion true.

In this sense, the hypothesis and conclusion describe two categories or sets to which things belong, and both statements imply that the hypothesis category is contained in the conclusion category. This can be represented by a Venn diagram:

 

For example: 

All A’s are B’s     or      If it is an A then it is a B

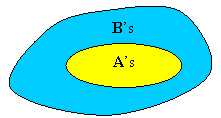both tell us that the A’s are a subset of the B’s:

toc | return to top | previous page | next page