In a previous lesson you learned that an exterior angle of any triangle is equal to the sum of the two remote interior angles:

Exterior angles of polygons also lead to important results.  Since an exterior angle is supplementary to its adjacent interior angle, its measure will be 180^o minus the measure of the adjacent interior angle. 

Using a little algebra, it can be seen from the above theorem that if you add the measures of a set of exterior angles of a polygon, one at each vertex, the sum will always be exactly 360^o:

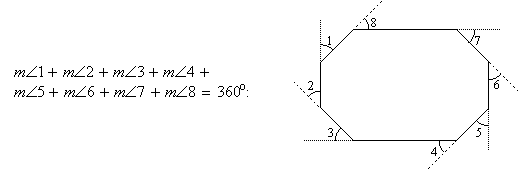
This result may seem a bit surprising, but if you imagine extending the sides of the exterior angles and moving very far away from the polygon so it appears as a dot, you get the following picture.  Then it seems obvious that the exterior angles add to 360^o: