. Notice that for the octagon above, it appears that angles A, B, C, D, E, and H are each 90o, while angles F and G are each 270o, and 
.Angles in Polygons
Filling a Polygon with Triangles
An important property of any polygon is that it can be completely filled with non-overlapping triangles with their vertices at the vertices of the polygon. For example, octagon ABCDEFGH on the left can be filled with 6 triangles as shown on the right:
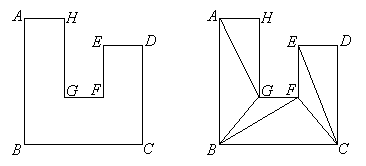
It takes exactly 6 triangles to fill the octagon this way, and the sum of the angle-measures of the octagon is equal to sum of the angle-measures of the triangles, which in this case is . Notice that for the octagon above, it appears that angles A, B, C, D, E, and H are each 90o, while angles F and G are each 270o, and .
A way to produce those triangles is to start at one of the vertices, draw segments other than sides of the polygon to as many other vertices as possible without going outside the polygon, then move to another vertex and connect as many vertices as possible that haven't already been connected, but with segments that do not cross other segments or go outside the polygon, and so on until the polygon is filled with triangles. In the above case, we started at vertex A and were able to draw only one segment, 
. Then we moved to vertex B and were able to draw segments 
and 
, but not 
or 
, because those segments would have gone outside the polygon (both would have cut side 
). Next we moved to vertex C and drew 
and 
. After that the polygon was filled.
Interior Angles in Convex Polygons
When the polygon is convex, this procedure leads us to construct all the triangles at one vertex of the polygon. For example, the octagon on the left can be filled with triangles sharing vertex A as on the right:
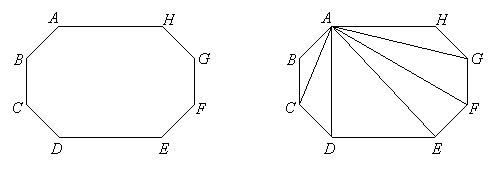
Notice that the number of segments that can be drawn is exactly 3 less than the number of vertices. In the above case, we cannot draw segments from vertex A to vertices B or H, because those segments are sides of the polygon, but we can draw segments from A to the remaining 5 vertices (C, D, E, F and G). Each segment we draw except the last produces one new triangle, and the last one gives us two triangles. Therefore, the number of triangles produced will be exactly two less than the number of vertices in the polygon, and since the number of vertices in a polygon is the same as the number of sides, we can state the following theorem about the angle-measures of any polygon:
THEOREM: The sum of the interior angles of a polygon consisting of n sides is equal to n – 2 times 180o.
Exterior Angles
In a previous lesson you learned that an exterior angle of any triangle is equal to the sum of the two remote interior angles:
Exterior angles of polygons also lead to important results. Since an exterior angle is supplementary to its adjacent interior angle, its measure will be 180o minus the measure of the adjacent interior angle.
Using a little algebra, it can be seen from the above theorem that if you add the measures of a set of exterior angles of a polygon, one at each vertex, the sum will always be exactly 360o:
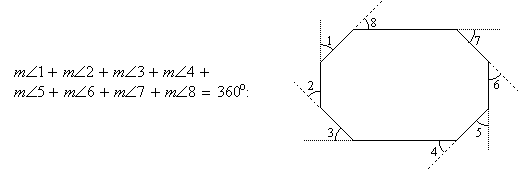
This result may seem a bit surprising, but if you imagine extending the sides of the exterior angles and moving very far away from the polygon so it appears as a dot, you get the following picture. Then it seems obvious that the exterior angles add to 360o:
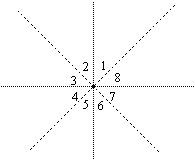
Here are a couple examples to show how these results can be used:
| EXAMPLE 1: | What is the sum of the measures of the interior angles of the polygon on the right? |  |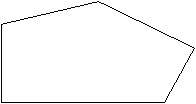
SOLUTION: This is a pentagon (5 sides) and can therefore be filled with 3 triangles, so the sum of its interior angles is 
.
| EXAMPLE 2: | What is the measure of each interior angle of a regular heptagon? |  |
SOLUTION: The exterior angles add to 360o, and there are 7 of them. Since it is a regular heptagon, the angles are all the same, so an exterior angle measures 
. Therefore each interior angle measures 
= 
.