An important property of any polygon is that it can be completely filled with non-overlapping triangles with their vertices at the vertices of the polygon.  For example, octagon ABCDEFGH on the left can be filled with 6 triangles as shown on the right:

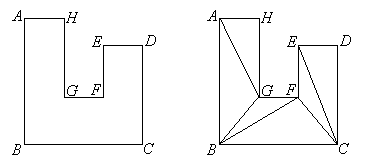
 It takes exactly 6 triangles to fill the octagon this way, and the sum of the angle-measures of the octagon is equal to sum of the angle-measures of the triangles, which in this case is .  Notice that for the octagon above, it appears that angles A, B, C, D, E, and H are each 90^o, while angles F and G are each 270^o, and .

 A way to produce those triangles is to start at one of the vertices, draw segments other than sides of the polygon to as many other vertices as possible without going outside the polygon, then move to another vertex and connect as many vertices as possible that haven't already been connected, but with segments that do not cross other segments or go outside the polygon, and so on until the polygon is filled with triangles.  In the above case, we started at vertex A and were able to draw only one segment, .  Then we moved to vertex B and were able to draw segments  and , but not or , because those segments would have gone outside the polygon (both would have cut side ).  Next we moved to vertex C and drew  and .  After that the polygon was filled.