When the polygon is convex, this procedure leads us to construct all the triangles at one vertex of the polygon.  For example, the octagon on the left can be filled with triangles sharing vertex A as on the right:

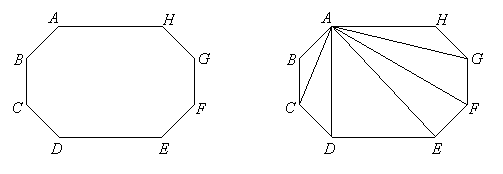
Notice that the number of segments that can be drawn is exactly 3 less than the number of vertices.  In the above case, we cannot draw segments from vertex A to vertices B or H, because those segments are sides of the polygon, but we can draw segments from A to the remaining 5 vertices (C, D, E, F and G).  Each segment we draw except the last produces one new triangle, and the last one gives us two triangles.  Therefore, the number of triangles produced will be exactly two less than the number of vertices in the polygon, and since the number of vertices in a polygon is the same as the number of sides, we can state the following theorem about the angle-measures of any polygon:

THEOREM:   The sum of the interior angles of a polygon consisting of n sides is equal to n – 2  times 180^o.