Example 4:  PR and QR are tangent to circle O.  Find the radius of circle O:

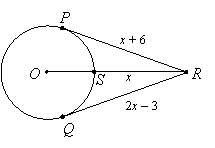Solution:  Since tangents from an external point are congruent, we can solve the equation

x + 6 = 2x – 3

to find x = 9.  Therefore RS = 9.  Now draw the radius from O to P and let its length be r.  Then OP = r and OS = r, and OP is perpendicular to PR:

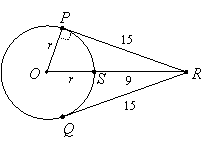Since triangle OPR is a right triangle, we can use the Pythagorean Theorem to find r:

r2 + 152 = (r + 9)2

r2 + 225 = r2 + 18r + 81

144 = 18r

r = 8

So the radius of circle O is 8 units.


toc | return to top | previous page | next page