Tangents
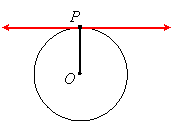
A Tangent is Perpendicular to a Radius and Diameter
A line tangent to a circle with center O at point P is perpendicular to the radius from O to P.
 |
If this were not true then we could draw a segment from O perpendicular to the line at some point Q:
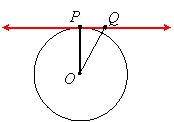 |
Then triangle OQP would be a right triangle with Q as the right angle and therefore OP as the hypotenuse. This would imply that OP is longer than OQ. But that can't be since Q is outside the circle and therefore OQ is longer than the radius.
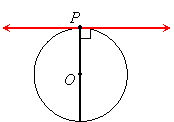
Since a diameter contains a radius, a line tangent to a circle is also perpendicular to the diameter that meets the point of tangency:
 |
Example 1: Determine whether line AB is tangent to circle O:
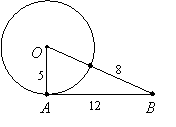 |
Solution: If it is tangent, then triangle OAB would be a right triangle. Since the radius of the circle is 5 units, the hypotenuse would be OB = 5 + 8 = 13. We check using the Pythagorean Theorem: 52 + 122 = 169 = 132. Since a2 + b2 = c2, it is a right triangle, so line AB is tangent to circle O.
Chord to Tangent
A more general result concerns the angles formed by any chord with an endpoint on the point of tangency:
If line RS is tangent to circle O at P and PA is a chord, then the measure of angle SPA is one-half the measure of arc PA and the measure of angle RPA is one-half the measure of arc PBA.

We can see why this is true as follows.
Draw diameter PC.

Then angle CPA is one-half the measure of arc AC. Since PC is perpendicular to the tangent line, angle SPA is complementary to this angle. Furthermore, the measure of arc PA is 180o minus the measure of arc CA since these arcs form a semicircle. Putting this together,
As for angle RPA, it is supplementary to angle SPA, and the measure of arc PA is 360o minus the measure of arc PBA, so
![]()
Example 2: Line AB is tangent to circle O, and angle ACB is a right angle. Find the lengths of AC and BC.
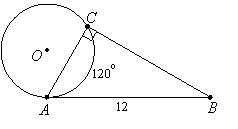 |
Solution: Angle CAB measures half of 120o, or 60o. Therefore triangle ACB is a 30-60-90 triangle, so AC is half the hypotenuse, or 6 units, and BC is AC times the square root of 3:
![]()
Example 3: Line RS is tangent to circles P and Q at points R and S. Find the length of segment RS.
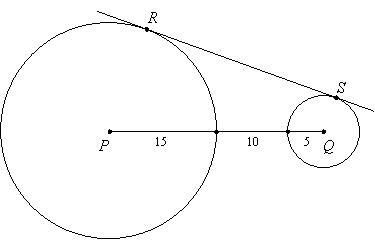 |
Solution: Draw radii from P to R and from A to S. These radii are perpendicular to the tangent line, and the total length of segment PQ is 30 units:
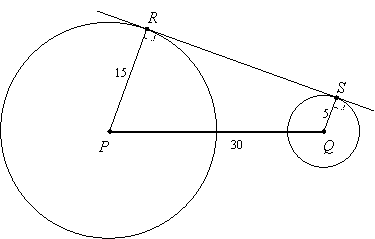
Now construct TS parallel to PQ to form parallelogram TSQP:
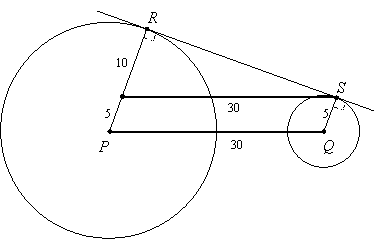 |
Then triangle TRS is a right triangle, so we can use the Pythagorean Theorem to find RS:
RS2 + 102 = 302
RS2 + 100 = 900
RS2 = 800
So RS is the square root of 800, which simplifies:
![]()
or approximately 28.28 units.
Tangents from an External Point
Tangent segments from a common point external to a circle have the same length.
 |
We can prove this as follows:
Let O be the center of the circle, P the common endpoint of the tangent segments, and A and B their points of tangency. Then angles OAP and OBP are right angles (because tangents are perpendicular to radii). Since segments OA and OB are radii, they are the same length. OP is a common hypotenuse of right triangles OAP and OBP, so these triangles are congruent by HL. Therefore AP = BP since they are corresponding parts.
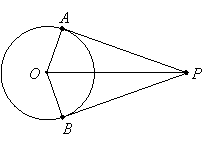 |
Example 4: PR and QR are tangent to circle O. Find the radius of circle O:
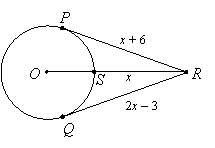 |
Solution: Since tangents from an external point are congruent, we can solve the equation
x + 6 = 2x – 3
to find x = 9. Therefore RS = 9. Now draw the radius from O to P and let its length be r. Then OP = r and OS = r, and OP is perpendicular to PR:
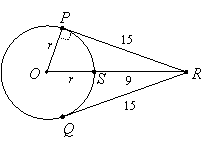 |
Since triangle OPR is a right triangle, we can use the Pythagorean Theorem to find r:
r2 + 152 = (r + 9)2
r2 + 225 = r2 + 18r + 81
144 = 18r
r = 8
So the radius of circle O is 8 units.
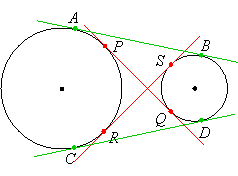
Common Tangents
Two non-overlapping circles have four common tangents. Two cross the segment joining the centers of the circle and are called internal tangents,
 |
and the other two do not cross this segment and are called external tangents.
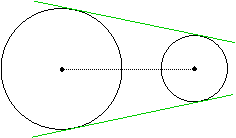
The lengths of the segments from their points of tangency are the same:
AB = CD and PQ = RS
Example 5: AB and CD are common external tangents to circles P and Q. What is the value of x?
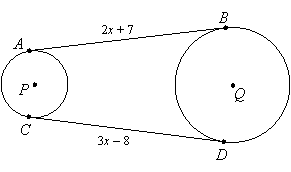 |
Solution: The common tangents are congruent, so we can solve the equation
2x + 7 = 3x – 8 to find that x = 15.
Return to Lesson 7