Tangents from an External Point

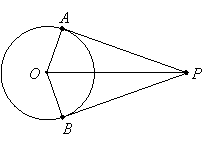
Tangent segments from a common point external to a circle have the same length. 

We can prove this as follows:

Let O be the center of the circle, P the common endpoint of the tangent segments, and A and B their points of tangency.  Then angles OAP and OBP are right angles (because tangents are perpendicular to radii).  Since segments OA and OB are radii, they are the same length.  OP  is a common hypotenuse of right triangles OAP and OBP, so these triangles are congruent by HL.  Therefore AP = BP since they are corresponding parts.

toc | return to top | previous page | next page